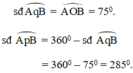Các câu hỏi tương tự
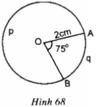
Trong hình 68, đường tròn tâm O có bán kính R = 2cm, góc A O B = 75 °
a) Tính sđ góc ApB
b) Tính độ dài hai cung AqB và ApB
c) Tính diện tích hình quạt tròn OAqB
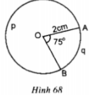
Trong hình 68, đường tròn tâm O có bán kính R = 2cm, góc AOB = 75o.
Tính diện tích hình quạt tròn OAqB
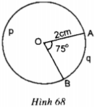
Trong hình 68, đường tròn tâm O có bán kính R = 2cm, góc AOB = 75o.
Tính độ dài hai cung AqB và ApB

a) Vẽ đường tròn tâm O, bán kính 2cm.
b) Vẽ hình vuông nội tiếp đường tròn (O) ở câu a).
c) Tính bán kính r của đường tròn nội tiếp hình vuông ở câu b) rồi vẽ đường tròn (O; r).
bài 1: cho đường tròn tâm /o bán kính 2cm. Góc SOB 60.a) tính sđ cung AmBb) tính độ dài hai cung AnB và AmB, độ dài đường tròn tâm Oc) tính diện tích hình tròn, diện tích hình quạt tròn OAnB.bài 2: cho tam giác ABC có 3 góc nhọn. Đừng tròn tâm O đường kính BC cắt AB, AC lần lượt tại I và K. BK và CI cắt nhua tại H. Tia AH cắt BC tại M.a) chứng minh AMperp BCb) chứng minh tứ giác BIHM, CMHK, AKMB nội tiếp. xác định tâm đường tròn ngoại tiếp
Đọc tiếp
bài 1: cho đường tròn tâm /o bán kính 2cm. Góc SOB =60.
a) tính sđ cung AmB
b) tính độ dài hai cung AnB và AmB, độ dài đường tròn tâm O
c) tính diện tích hình tròn, diện tích hình quạt tròn OAnB.
bài 2: cho tam giác ABC có 3 góc nhọn. Đừng tròn tâm O đường kính BC cắt AB, AC lần lượt tại I và K. BK và CI cắt nhua tại H. Tia AH cắt BC tại M.
a) chứng minh \(AM\perp BC\)
b) chứng minh tứ giác BIHM, CMHK, AKMB nội tiếp. xác định tâm đường tròn ngoại tiếp
Vẽ đường tròn tâm O bán kính R=2cm rồi vẽ hình tám cạnh đều nội tiếp đường tròn (O;2cm) .Nêu cách vẽ
BT1: Trên đường tròn (O; R) lấy A,B,C sao cho dây AC=R, dây BC= R √ 2, tia CO nằm giữa tia CA và CB. Tính sđ các GÓC: AOC, COB, AOB. Tính sđ cung BC
BT2: Cho tam giác ABC cân tại A, góc A nhọn. Đường tròn (O), đường kính BC cắt AB, AC tại D và E.
CM: BE = CD ⇒ góc BDE = góc DEC.
CM: cung CE = cung BD
Cho đường tròn tâm O bán kính R có đường kính AB cố định. Vẽ đường kính MN của đường tròn tâm O bán kính R (M khác A ,M khác B). Tiếp tuyến của dường tròn tâm o bán kính r tại B cắt đường thẳng AM AN lần lượt tại Q và P
a, Cm tg AMNB Là hình chữ nhật
b, chứng minh 4 điểm M, N, P, Q cùng thuộc 1 đường tròn
Cho đường tròn tâm O bán kính R. Vẽ góc ở tâm AOB = 80 ° , vẽ góc ở tâm BOC = 120 ° kề với góc AOB. So sánh và sắp xếp độ dài AB, BC, CA theo thứ tự tăng dần.