Cho tam giác ABC. Nếu a = 2b thì
A. h b = 2 h a
B. h b = h a
C. h a = 2 h b
D. h b = 4 h a
Cho tam giác AB, các đường cao tương ứng với a, b, c theo thứ tự là ha, hb, hc
Chứng minh rắng : nếu \(\frac{1}{h^2a}=\frac{1}{h^2b}+\frac{1}{h^2c}\)
thì tam giác ABC là tam giác vuông
Cho tam giác ABC có c^h-2a^2c^2-2b^2c^2+a^2+a^2b^2+b^4. Tính cos C
cho tam giác abc biết ab=18cm, ac=24cm, bc=32cm. Gọi ha, hb,hc là độ dài 3 đường cao tương ứng. CMR nếu lấy hc,hb,ha theo thứ tự làm độ dài 3 cạnh thì ta được tam giác mới đồng dạng với tam giác abc theo một thứ tự đỉnh nào đó.
Các câu sau đúng hay sai?
a) Nếu tam giác ABC vuông tại C thì điểm C thuộc đường tròn có đường kính là AB (h.88)
b) Nếu điểm C thuộc đường tròn có đường kính là AB (C khác A và B) thì tam giác ABC vuông tại C (h.89).
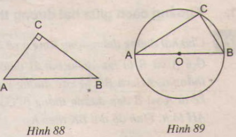
a) Đúng
Gọi O là trung điểm của AB.
Ta có CO là trung tuyến ứng với cạnh huyền nên
⇒ OC = AB/2 = OA = OB.
⇒ A, B, C cùng thuộc đường tròn bán kính OA.
Tâm O là trung điểm của AB nên AB là đường kính.
Vậy C thuộc đường tròn đường kính AB.
b) Đúng
Gọi O là tâm đường tròn.
⇒ OA = OB = OC = R
AB là đường kính nên AB = 2R.
Tam giác ABC có CO là trung tuyến và CO = AB/2
⇒ ΔABC vuông tại C.
cho tam giác ABC có AB=c, BC=a, AC=b. Chu vi bằng 2p. Các đường cao tương ứng:h,m,n (AH=h, BK=m, CI=n). CMR:
a) (b+c)^2 > hoặc bằng a^2 + 4h^2
b)h^2 < hoặc bằng p.(p-a)
c) h^2 + m^2 + n^2 < hoặc bằng p^2
Nếu a + ha = b + hb = c + hc thì tam giác AbC là tam giác đều
P/s chứng minh bằng phương pháp phản chứng
Cho tam giác ABC cân A
a) Biết góc B =60 độ
b) Kẻ AH vuông góc BC (H thuộc BC).CM: H là trung điểm BC
c) Biết AH=4cm, BC= 6cm.Tính AB
d) Nếu góc HAC = 30 độ thì tam giác ABC là tam giác gì ? Vì sao
cho tam giác ABC biết 2 đỉnh và trực tâm H. Lập phương trình các cạnh của tam giác ABC trong các trường hợp sau
a) A(1;1), B(3;4), H(0;0)
b) A(-1;2), B(-2;-2), H(3;2)
Cách làm 2 câu tương tự nhau.
a.
\(\overrightarrow{AB}=\left(2;3\right)\Rightarrow\) đường thẳng AB nhận (3;-2) là 1 vtpt
Phương trình AB (qua A) có dạng:
\(3\left(x-1\right)-2\left(y-1\right)=0\Leftrightarrow3x-2y-1=0\)
\(\overrightarrow{HA}=\left(1;1\right);\overrightarrow{HB}=\left(3;4\right)\)
Do BC vuông góc AH nên nhận (1;1) là 1 vtpt
Phương trình BC (đi qua B) có dạng:
\(1\left(x-3\right)+1\left(y-4\right)=0\Leftrightarrow x+y-7=0\)
Do AC vuông góc HB nên nhận (3;4) là 1 vtpt
Phương trình AC (đi qua A) có dạng:
\(3\left(x-1\right)+4\left(y-1\right)=0\Leftrightarrow3x+4y-7=0\)
Câu b hoàn toàn tương tự
cho tam giác ABC nhọn, đường cao BD,CE. Gọi H,K là hình chiếu của B,C trên đường thẳng DE a) CMR: HE=KC b) Nếu tam giác ABC cân tại A thì tứ giác BCKH là hình gì GIÚP MK VỚI
Bn xem cái này nhé :

Ủng hộ mk nhé :
Chúc bn học tốt
Giúp mih mấy bài này nhà.Mih đang cần gấp. Mình sẽ cảm ơn những người đã giúp mih
6. Cho tam giác ABC có góc A và góc B tỉ lệ với 3 và 15; góc C gấp 4 lần góc A. Tính các góc của tam giác ABC.
7. Cho tam giác AHB và tam giác A’H’B’ vuông tại H và H’; với AH = A’H’ và góc B bằng góc B’. Kéo dài BH và B’H’ ra những đoạn HC = H’C’. Chứng minh rằng tam giác ABC bằng tam giác A’B’C’.
8. Cho tam giác ABC và tam giác A’B’C’ với các tia phân giác của góc A và góc A’ cắt BC và B’C’ tại D và D’. Chứng minh rằng nếu AD = A’D’ , góc A bằng góc A’ và góc C bằng góc C’ thì hai tam giác đó bằng nhau.
9. Cho tam giác ABC cân tại A và tam giác A’B’C’ cân tại A’. Vẽ AH và A’H’ lần lượt vuông góc với BC và B’C’ lần lượt tại H và H’. Chứng minh rằng nếu AH = A’H’ , góc A bằng góc A’ thì hai tam giác đó bằng nhau.
10. Cho tam giác ABC có AB<AC. M là trung điểm BC. Từ M vẽ đường thẳng vuông góc với tia phân giác góc A tại N và cắt AB tại E, cắt AC tại F. Chứng minh rằng:
a. AE=AF b. BE=CF c. AB+AC=2AE.