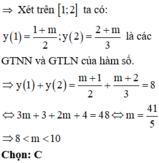Giá trị lớn nhất của hàm số y = 2 mx + 1 m - x trên 2 ; 3 là - 1 3 khi m nhận giá trị bằng:
A. -5
B. 1
C. 0
D. -2
Cho hàm số y = m x + 1 2 x − 1 (m là tham số, m ≠ 2 ). Gọi a, b lần lượt giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên 1 ; 3 . Khi đó có bao nhiêu giá trị của m để a . b = 1 5 .
A. 0
B. 2
C. 1
D. 3
Đáp án B
Tập xác định: D = ℝ \ 1 2 ⇒ Hàm số y = m x + 1 2 x − 1 liên tục và đơn điệu trên 1 ; 3
⇒ a . b = y 1 . y 3 = m + 1 1 . 3 m + 1 5 = 1 5
⇔ m + 1 3 m + 1 = 1 ⇔ 3 m 2 + 4 m = 0 ⇔ m = 0 m = − 4 3
Vậy có 2 giá trị m thỏa mãn.
cho hàm số y=mx^2+(3m-1)x+2m-3. Gọi A là giá trị nhỏ nhất của hàm số. Tìm m sao cho A đạt giá trị lớn nhất
Cho hàm số y = m x + 1 2 x − 1 (m là tham số, m ≠ 2 ). Gọi a, b lần lượt giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên [1;3]. Khi đó có bao nhiêu giá trị của m để a . b = 1 5 .
A. 0
B. 2
C. 1
D. 3
Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số y = x 2 + m x + m x + 1 trên [1;2] bằng 2. Số phần tử của S là
A. 1
B. 4
C. 3
D. 2
Gọi S là tập hợp tất cả các giá trị thực của m sao cho giá trị lớn nhất của hàm số y = x 2 + m x + m x + 1 trên đoạn [ 1 ; 2 ] bằng 2. Số phần tử của tập S là:
A. 3
B. 1
C. 4
D. 2
Đáp án D.
Xét hàm số f x = x 2 + m x + m x + 1 trên 1 ; 2 , có y ' = x 2 + 2 x x + 1 2 > 0 , ∀ x ∈ 1 ; 2
Suy ra
max 1 ; 2 f x = f 1 ; f 2 = 2 m + 1 2 ; 3 m + 4 3 = 2 m + 1 2 ; 3 m + 4 3
TH1. Với
max 1 ; 2 f x = 2 m + 1 2 = 2 m + 1 = 4 2 m + 1 2 ≥ 3 m + 4 3 ⇔ m = − 5 2 .
TH2:
Với max 1 ; 2 f x = 3 m + 4 3 = 3 m + 4 = 6 2 m + 1 2 ≤ 3 m + 4 3 ⇔ m = 2 3 .
Giá trị lớn nhất của hàm số y = x 3 + x 2 - m x + 1 trên 0 ; 2 bằng 5. Tham số m nhận giá trị là:
A. - 5
B. 1
C. - 3
D. - 8
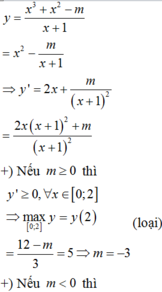
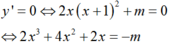
có nhiều nhất 1 nghiệm trên đoạn 0 ; 2
(do
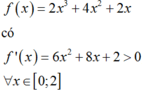
Ta có:
![]()
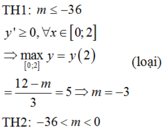
Phương trình y ' = 0 có 1 nghiệm duy nhất x 0 ∈ 0 , 2 và đổi dấu tại điểm này
Bảng biến thiên:
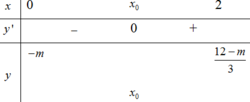
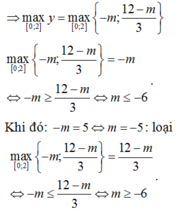
Khi đó:
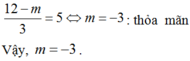
Chọn C.
tìm tổng tất cra các giá trị của tham số thực m để hàm số y=|mx-1|-x^2 có giá trị lớn nhất bằng 10/8
Với giá trị nào của m thì hàm số y = m x − 1 x + m đạt giá trị lớn nhất bằng 1 3 trên 0 ; 2 .
A. m=1
B. m=3
C.m=-3
D.m=-1
Đáp án A
Ta có y ' = m 2 + 1 x + m 2 > 0 với ∀ x ∈ T X D . Để hàm số đạt giá trị lớn nhất bằng 1 3 trên 0 ; 2 điều kiện cần và đủ là y 2 = 1 3 ⇔ 2 m − 1 2 + m = 1 3 ⇒ m = 1
Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x + m x + 1 trên [1;2] bằng 8 (m là tham số thực). Khẳng định nào sau đây đúng?
A. m > 10
B. 8 < m < 10
C. 0 < m < 4
D. 4 < m < 8
Chọn B
Nếu m = 1 thì y = 1 (không thỏa mãn tổng của giá trị lớn nhất và nhỏ nhất bằng 8)
Nếu m
≠
1 thì hàm số đã cho liên tục trên [1;2] và 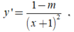
Khi đó đạo hàm của hàm số không đổi dấu trên đoạn [1;2]
Do vậy ![]()
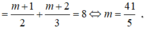
Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x + m x + 1 trên đoạn [1;2] bằng 8 (m là tham số thực). Khẳng định nào sau đây là đúng?
A. 0 < m < 4
B. 4 < m < 8
C. 8 < m < 10
D. m > 10

Vì hàm số đã cho là hàm bậc nhất trên bậc nhất nên hàm số đơn điệu trên từng khoảng xác định của hàm số.