Tìm mệnh đề sai trong các mệnh đề sau
A. Giá trị nhỏ nhất của hàm số y = 2 x + 2 x - 2 bằng 4
B. Hàm số y = 2 3 - x nghịch biến trên R
C. Hàm số y = log 2 x 2 + 1 đồng biến trên R
D. Hàm số y = log 1 2 x 2 + 1 đạt cực đại tại x = 0
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = sin 5 x + 3 cos x . Trong các mệnh đề sau mệnh đề nào là sai?
A. M + m = 0
B. Mn = -3
C. M - m = 2 3
D. M m = 1
Chọn D

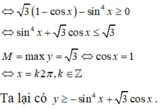
Tương tự như trên, áp dụng bất đẳng thức Cauchy ta có
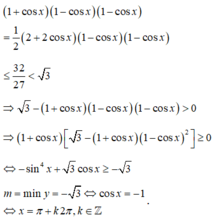
Do đó 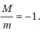 . Vì vậy, mệnh đề D sai.
. Vì vậy, mệnh đề D sai.
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = sin 5 x + 3 cos x . Trong các mệnh đề sau mệnh đề nào là sai?
A. M + m = 0
B. Mm = -3
C. M - m = 2 3
D. M m = 1
Ta có
sin 5 x ≤ sin 4 x ⇒ y ≤ sin 4 x + 3 cos x
Áp dụng bất đẳng thức Cauchy ta có:
1 - cos x 1 + cos x 1 + cos x = 1 2 2 - 2 cos x 1 + cos x 1 + cos x
≤ 1 2 2 - 2 cos x + ( 1 + cos x ) 2 3 3 = 32 27 < 3
⇒ 3 - 1 - cos x 1 + cos x 2 > 0 ⇒ 1 - cos x 3 - 1 - cos x 1 + cos x 2 ≥ 0 ⇒ 3 1 - cos x - sin 4 x ≥ 0 ⇔ sin 4 x + 3 cos x ≤ 3
M = maxy = 3 ⇔ cos(x) = 1
⇔ x = k 2 π , k ∈ ℤ
Ta lại có
y ≥ - sin 4 x + 3 cos x
Tương tự như trên, áp dụng bất đẳng thức Cauchy ta có:
1 + cos x 1 - cos x 1 - cos x = 1 2 2 + 2 cos x 1 - cos x 2 ≥ 32 27 ≤ 3 ⇒ 3 - 1 + cos x 1 - cos x 2 > 0 ⇒ 1 + cos x 3 - 1 + cos x 1 - cos x 2 ⇔ sin 4 x + 3 cos x ≥ - 3 m = m i n y = - 3 ⇔ cos x = - 1 ⇔ x = k 2 π , k ∈ ℤ
Do đó M m = - 1 . Vì vậy, mệnh đề D sai.
Đáp án cần chọn là D
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = sin x - cos 2 x . Hỏi mệnh đề nào trong các mệnh đề sau là sai?
A. 2 M m = 2
B. M + m = 2
C. M m = 0
D. M - m = 2
Ta có
y = sin x = cos 2 x = sin x - 1 - 2 sin 2 x = 2 sin 2 x + sin x - 1
Đặt t = sin(x), - 1 ≤ t ≤ 1
Ta sẽ đi tìm GTLN và GTNN của hàm số y = g t = 2 t 2 + t - 1 trên đoạn [ -1;1 ]
Ta có g t = - 2 t 3 - t + 1 , - 1 ≤ t ≤ 1 2 2 t 3 + t - 1 , 1 2 ≤ t ≤ 1
* Xét hàm số h t = - 2 t 3 - t + 1 trên đoạn - 1 ; 1 2
Dễ dàng tìm được
M a x r ∈ 1 2 ; 1 h t = 9 8 ⇔ t = - 1 4 M i n r ∈ 1 2 ; 1 h t = 0 ⇔ t = 1 2
* Xét hàm số k t = 2 t 3 + t - 1 trên đoạn 1 2 ; 1
Cũng dễ dàng tìm được
M a x r ∈ 1 2 ; 1 k t = 2 ⇔ t = 1 M i n r ∈ 1 2 ; 1 k t = 0 ⇔ t = 1 2
Qua hai trường hợp trên ta đi đến kết luận
M a x r ∈ - 1 ; 3 g t = 2 ⇔ t = 1 M i n r ∈ - 1 ; 3 g t = 0 ⇔ t = 1 2
Hay
M = M a x y = 2 ⇔ sin x = - 1 ⇔ x = - π 2 + k 2 π m = Miny = 0 ⇔ sin x = 1 2 ⇔ x = π 6 + k 2 π x = 5 π 6 + k 2 π
Đáp án C
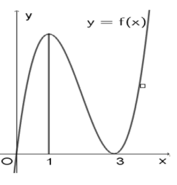
Cho hàm số y = f(x) có đồ thị như hình vẽ bên dưới . Để đồ thị hàm số h(x) = | f 2 ( x ) + f ( x ) + m | có số điểm cực trị ít nhất thì giá trị nhỏ nhất của tham số m = m o . Tìm mệnh đề đúng trong các mệnh đề sau:
![]()
![]()
![]()
![]()
Cho hàm số y= f(x) có đồ thị như hình vẽ bên dưới . Để đồ thị hàm số h(x) = f 2 ( x ) + f ( x ) + m có số điểm cực trị ít nhất thì giá trị nhỏ nhất của tham số m = m o
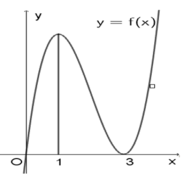
Tìm mệnh đề đúng trong các mệnh đề sau
A.![]()
B. ![]()
C. ![]()
D. ![]()
Đồ thị hàm số y = f x có bảng biến thiên như hình vẽ
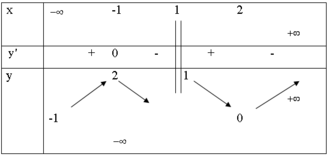
Xét các mệnh đề sau
(I) Đồ thị hàm số không có tiệm cận ngang
(II) Đồ thị hàm số không có tiệm cận đứng
(III) Giá trị lớn nhất của hàm số bằng 2
(IV) Giá trị nhỏ nhất của hàm số bằng 0
Số mệnh đề đúng là:
A. 3
B. 0
C. 2
D. 1
Đáp án B
Dựa vào bảng biến thiên ta thấy:
+) lim x → − ∞ y = − 1 ⇒ đồ thị hàm số có TCN y = − 1
+) lim x → 1 − y = − ∞ ⇒ đồ thị hàm số có TCĐ x = 1
+) Hàm số không có giá trị lớn nhất vì lim x → + ∞ y = + ∞
+) Hàm số không có giá trị nhỏ nhất vì lim x → 1 − y = − ∞
Suy ra không có mệnh đề nào đúng
Cho hàm số y = f ( x ) liên tục trên ℝ và có đồ thị như hình vẽ bên. Xét 4 mệnh đề sau
(1) Hàm số y = f ( x ) đạt cực đại tại x 0 = 0
(2) Hàm số y = f ( x ) có ba cực trị.
(3) Phương trình y = f ( x ) có đúng ba nghiệm phân biệt
(4) Hàm số đạt giá trị nhỏ nhất là -2 trên đoạn [-2;2]
Hỏi trong 4 mệnh đề trên, có bao nhiêu mệnh đề đúng?

A. 1
B. 3
C. 4
D. 2
Đáp án D
Hàm số y = f ( x ) đạt cực tiểu tại x 0 = 0
Hàm số y = f ( x ) có ba điểm cực trị.
Phương trình f ( x ) = 0 có 4 nghiệm phân biệt
Hàm số đạt giá trị nhỏ nhất là -2 trên đoạn [-2;2]
Cho hàm số y=f(x) liên tục trên ℝ và có đồ thị như hình dưới đây:
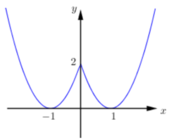
Xét các mệnh đề sau:
(I). Hàm số nghịch biến trên khoảng
(II). Hàm số đồng biến trên khoảng
(III). Hàm số có ba điểm cực trị
(IV). Hàm số có giá trị lớn nhất bằng 2.
Số mệnh đề đúng trong các mệnh đề trên là:
A. 4
B. 2
C. 3
D. 1
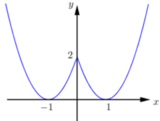
Cho hàm số y=f(x) liên tục trên R và có đồ thị như hình dưới đây:
Xét các mệnh đề sau:
(I). Hàm số nghịch biến trên khoảng (0;1)
(II). Hàm số đồng biến trên khoảng (-1;2)
(III). Hàm số có ba điểm cực trị
(IV). Hàm số có giá trị lớn nhất bằng 2.
Số mệnh đề đúng trong các mệnh đề trên là:
A. 4
B. 2
C. 3
D. 1
Chọn đáp án B
Phương pháp
Dựa vào đồ thị hàm số xác định các khoảng đơn điệu, các điểm cực trị và GTLN, GTNN của hàm số.
Cách giải
Dựa vào đồ thị hàm số ta thấy hàm số đã cho
+) Đồng biến trên (-1;0) và (1;+∞), nghịch biến trên (-∞;-1) và (0;1).
+) Hàm số có 3 điểm cực trị.
+) Hàm số không có GTLN.
Do đó các mệnh đề (I), (III) đúng.
Cho đồ thị (C) của hàm số y' = ( 1 + x ) x + 2 2 x - 3 3 ( 1 - x 2 ) . Trong các mệnh đề sau, tìm mệnh đề sai:
A. (C) có một điểm cực trị.
B. (C) có ba điểm cực trị.
C. (C) có hai điểm cực trị.
D. (C) có bốn điểm cực trị.
Chọn C.
Ta có y' = ( 1 + x ) x + 2 2 x - 3 3 ( 1 - x 2 ) nên y' = 0
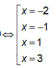
Bảng xét dấu
![]()
Ta thấy đạo hàm đổi dấu 2 lần nên hàm số có hai điểm cực trị suy ra đồ thị hàm số có 2 điểm cực trị.
Trắc nghiệm: Ta thấy phương trình y' = 0 có 2 nghiệm đơn hoặc bội lẻ nên đồ thị hàm số có hai điểm cực trị.