Người ta đặt một khối chóp tứ giác đều lên trên một khối lập phương để thu được một khối mới như trong hình. Tính thể tích V của khối mới thu được?
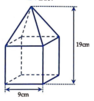
A. V=513 c m 3
B. V=999 c m 3
C. V=1242 c m 3
D. V=1539 c m 3
Người ta đặt một khối chóp tứ giác đều lên trên một khối lập phương để thu được một khối mới như trong hình. Tính thể tích V của khối mới thu được?
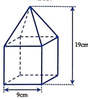
A. V=513 (cm3)
B. V=999 (cm3)
C. V=1242 (cm3)
D. V=1539 (cm3)
Đáp án B
+ Thể tích của khối lập phương bằng 9 3 = 729 (cm3).
+ Khối chóp tứ giác đều có cạnh đáy bằng 9 (cm) và chiều cao bằng 19-9=10 (cm). Do đó khối chóp có thể tích bằng 1 3 . 9 2 . 10 = 270 (cm3).
+ Vậy khối vật thể có thể tích bằng 729+270=999 (cm3).
Cho khối lập phương ABCD.A’B’C’D’. Cắt khối lập phương trên bởi các mặt phẳng (AB’D’) và (C’BD) ta được ba khối đa diện. Xét các mệnh đề sau:
(I): Ba khối đa diện thu được gồm hai khối chóp tam giác đều và một khối lăng trụ tam giác.
(II): Ba khối đa diện thu được gồm hai khối tứ diện và một khối bát diện đều
(III): Trong ba khối đa diện thu được có hai khối đa diện bằng nhau
Số mệnh đề đúng là:
A. 2
B. 1
C. 3
D. 0
Chọn B
Phương pháp:
Chia khối lập phương, nhận xét các khối tạo thành và tính thể tích của chúng
Cách giải:
Chia khối lập phương ABC.A’B’C’ bởi mặt phẳng (AB’D’) và (C’BD) ta được:
+) Chóp A.A’B’D’
+) Chóp C’.BCD
+) Khối bát diện ABD.B’C’D’
Ta có
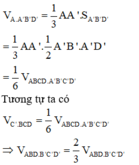
Các khối A.A’B’D’ và C’.BCD không phải là chóp tam giác đều và khối bắt diện ABD.B’C’D’ không phải là khói bát diện đều
Do đó chỉ có mệnh đề III đúng
Cho khối lập phương ABCD.A'B'C'D'. Cắt khối lập phương bởi các mặt phẳng (AB'D') và (C'BD) ta được ba khối đa diện. Xét các mệnh đề sau:
(I): Ba khối đa diện thu được gồm hai khối chóp tam giác đều và một khối lăng trụ tam giác.
(II): Ba khối đa diện thu được gồm hai khối tứ diện và một khối bát diện đều.
(III): Trong ba khối đa diện thu được có hai khối đa diện bằng nhau.
Số mệnh đề đúng là
A. 3.
B. 2.
C. 0.
D. 1.
Cho khối lập phương ABCD.A’B’C’D’. Cắt khối lập phương bởi các mặt phẳng (AB’D’) và (C’BD) ta được ba khối đa diện. Xét các mệnh đề sau:
(I): Ba khối đa diện thu được gồm hai khối chóp tam giác đều và một khối lăng trụ tam giác.
(II): Ba khối đa diện thu được gồm hai khối tứ diện và một khối bát diện đều.
(III): Trong ba khối đa diện thu được có hai khối đa diện bằng nhau.
Số mệnh đề đúng là
A. 3
B. 2
C. 0
D. 1
Cho khối chóp tứ giác đều S.ABCD có thể tích là V. Nếu tăng độ dài cạnh đáy lên ba lần và giảm độ dài đường cao xuống hai lần thì ta được khối chóp mới có thể tích là
A. 9 2 V
B. 9V
C. 3V
D. 3 2 V
Cho khối chóp tứ giác đều S . A B C D có thể tích là V. Nếu tăng độ dài cạnh đáy lên ba lần và giảm độ dài đường cao xuống hai lần thì ta được khối chóp mới có thể tích là
A. 9 2 V
B. 9 V
C. 3 V
D. 3 2 V
Đáp án A
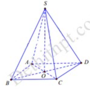
Kí hiệu như hình vẽ với S O ⊥ A B C D và tứ giác ABCD là hình vuông.
Ta có V = 1 3 S O . S A B C D = 1 3 S O . A B 2
Thể tích mới V ' = 1 3 . 1 2 S O . 3 A B 2 = 9 2 V
Cho khối chóp tứ giác đều S.ABCD có thể tích là V. Nếu tăng độ dài cạnh đáy lên ba lần và giảm độ dài đường cao xuống hai lần thì ta được khối chóp mới có thể tích là:
A. 9 2 V
B. 9V
C. 3V
D. 3 2 V
Đáp án A
Diện tích đáy tăng lên 9 lần và độ dài đường cao xuống hai lần. Khi đó thể tích khối chóp mới là 9 2 V
Cho khối chóp tứ giác đều S.ABCD có thể tích là V. Nếu tăng độ dài cạnh đáy lên ba lần và giảm độ dài đường cao xuống hai lần thì ta được khối chóp mới có thể tích là:
A. 9 2 V
B. 9 V
C. 3 V
D. 3 2 V
Cho một tấm nhôm hình vuông cạnh 1 (m) như hình vẽ dưới đây. Người ta cắt phần tô đậm của tấm nhôm rồi gập thành một hình chóp tứ giác đều có cạnh đáy bằng x (m). Tìm giá trị của x để khối chóp nhận được có thể tích lớn nhất.
A . x = 2 4
B . x = 2 3
C . x = 2 2 5
D . x = 1 2