Mỗi bạn An , Bình chọn ngẫu nhiên 3 chữ số trong tập 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 .  Tính xác suất để trong hai bộ ba chữ số mà An, Bình chọn ra có đúng một chữ số giống nhau.

A.  7 40

B. 9 10

C. 6 25

D.  21 40

Mỗi bạn An và Bình chọn ngẫu nhiên ba số trong tập {0,1,2,3,4,5,6,7,8,9}. Xác suất để trong hai bộ ba số của An và Bình chọn ra có nhiều nhất một số giống nhau bằng

A.-10

B. 203 480

C. 49 60

D. 17 24

Mỗi bạn An và Bình chọn ngẫu nhiên ba số trong tập {0,1,2,3,4,5,6,7,8,9}. Xác suất để trong hai bộ ba số của An và Bình chọn ra có nhiều nhất một số giống nhau bằng

Mỗi bạn An và Bình chọn ngẫu nhiên ba số trong tập {0,1,2,3,4,5,6,7,8,9}. Tính xác suất để trong hai bộ ba số của An và Bình chọn ra có nhiều nhất một số giống nhau bằng:

A .   - 10

B .   203 480

C .   49 60

D .   17 24

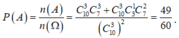
Cho tập hợp A   =   0 ;   1 ;   2 ;   3 ;   4 ;   5 . Gọi S là tập hợp các số có 3 chữ số khác nhau được tạo thành từ các chữ số của tập A. Chọn ngẫu nhiên một số từ S , xác suất để số được chọn có chữ số cuối gấp đôi chữ số đầu bằng

A.   23 25 .

B.   2 25 .

C.   4 5 .

D.   1 5 .

Tập S gồm các số tự nhiên có 6 chữ số khác nhau được thành lập từ các chữ số 0; 1; 2; 3; 4; 5; 6; 7; 8. Chọn ngẫu nhiên một số từ tập S. Xác suất để số được chọn không có hai chữ số chẵn đứng cạnh nhau là:

A.  11 70

B.  29 140

C.  13 80

D.  97 560

Gọi A là tập hợp các số tự nhiên có 6 chữ số đội một khác nhau được tạo ra từ các chữ số 0, 1, 2, 3, 4, 5. Từ A chọn ngẫu nhiên một số. Tính xác suất để số được chọn có chữ số 3 và 4 đứng cạnh nhau.

A. 4 25

B. 4 15

C.  8 15

D.  2 15

Gọi A là tập các số tự nhiên có 6 chữ số đôi một khác nhau được tạo ra từ các chữ số 0, 1, 2, 3, 4, 5. Từ A chọn ngẫu nhiên một số. Tính xác suất để số được chọn có chữ số 3 và chữ số 4 đứng cạnh nhau

A.  4 25 .

B.  4 15 .

C.  8 25 .

D.  2 15 .

Gọi A là tập các số tự nhiên có 6 chữ số đôi một khác nhau được tạo ra từ các chữ số 0, 1, 2, 3, 4, 5. Từ A chọn ngẫu nhiên một số. Tính xác suất để số được chọn có chữ số 3 và chữ số 4 đứng cạnh nhau.