Tập nghiệm của bất phương trình x ln x + e ln 2 x ≤ 2 e 4 có dạng S = [a; b]. Tích a.b bằng
A. 1
B. e
C. e 3
D. e 4
Tìm tập nghiệm của bất phương trình ( 2 x - 7 ) ln ( x + 1 ) > 0
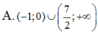
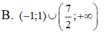
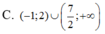
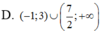
Cho hàm số f ( x ) = l n ( x 2 - 2 x + 3 ) . Tập nghiệm của bất phương trình f'(x)>0 là
A. ( 2 ; + ∞ ) .
B. ( - 1 ; + ∞ ) .
C. ( - 2 ; + ∞ ) .
D. ( 1 ; + ∞ ) .
Cho hàm số y = f ( x ) = ln ( 1 + x 2 + x ) .
Tập nghiệm của bất phương trình
f ( a - 1 ) + f ( ln a ) ≤ 0 là:
![]()
![]()
![]()
![]()
Tìm tập nghiệm của bất phương trình ln x 2 < 0
A. S = (-1;1)
B. S = (0;1)
C. S = (-1;0)
D. S = (-1;1)\{0}
Điều kiện: ![]()
Bất phương trình ![]()
Đối chiếu điều kiện ta được tập nghiệm S = (-1;1)\{0}
Chọn D.
Tập nghiệm của bất phương trình ln x 2 < 0 là
A. (-1,1)
B. (0,1)
C. (-1,0)
D. ( - 1 , 1 ) \ { 0 }
Tìm tập nghiệm S của bất phương trình ln x 2 < 0
A. S = (-1; 1)
B. S = (0; 1)
C. (-1; 0)
D. ( - 1 ; 1 ) \ { 0 }
Bất phương trình ln(2x2 + 3) > ln(x2 + ax + 1) nghiệm đúng với mọi số thực x khi:
A. - 2 2 < a < 2 2
B. 0 < a < 2 2
C. 0 < a < 2
D. - 2 < a < 2
Đáp án D
Ta có ln(2x2 + 3) > ln(x2 + ax + 1)
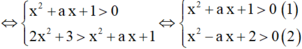
Giải (1), ta có x2 + ax + 1 > 0
∀ x ∈ ℝ ⇔ ∆ = a 2 - 4 < 0 ⇔ - 2 < a < 2 .
Giải (2), ta có x2 + ax + 2 > 0
∀ x ∈ ℝ ⇔ ∆ = - a 2 - 8 < 0 ⇔ - 2 2 < a < a 2 .
Vậy a thuộc (–2;2) là giá trị cần tìm.
Tập nghiệm của bất phương trình 2 x 2 − 4 − 1 . ln ( x 2 ) < 0 là
A. S = [ 1 ; 2 ] .
B. S = { 1 ; 2 } .
C. S = ( 1 ; 2 ) .
D. S = ( − 2 ; − 1 ) ∪ ( 1 ; 2 ) .
Đáp án D.
Cách 1: Tư duy tự luận
Điều kiện: x 2 > 0 ⇔ x ≠ 0.
Bất phương trình
( 2 x 2 − 4 − 1 ) . ln ( x 2 ) < 0 ⇔ 2 x 2 − 4 − 1 < 0 ln ( x 2 ) > 0 2 x 2 − 4 − 1 > 0 ln ( x 2 ) < 0 ⇔ x 2 − 4 < 0 x 2 > 1 x 2 − 4 > 0 x 2 < 1 ( L )
⇔ ( x − 2 ) ( x + 2 ) < 0 ( x − 1 ) ( x + 1 ) > 0 ⇔ − 2 < x < 2 x > 1 x < − 1 ⇔ 1 < x < 2 − 2 < x < − 1
Vậy tập nghiệm của bất phương trình là S = ( − 2 ; − 1 ) ∪ ( 1 ; 2 ) .
Cách 2: Sử dụng máy tính cầm tay
Nhập vào màn hình biểu thức 2 x 2 − 4 − 1 . ln ( X 2 ) và CALC với X = − 2 ; − 1 ; 1 ; 2.

Ta xét dấu của biểu thức 2 X 2 − 4 − 1 . ln ( X 2 ) trên mỗi khoảng ( − ∞ ; − 2 ) , ( − 2 ; − 1 ) , ( − 1 ; 1 ) , ( 1,2 ) , ( 2 ; + ∞ ) .
Tiếp tục dùng CACL:

Vậy
( 2 x 2 − 4 − 1 ) . ln ( x 2 ) < 0 ⇔ x ∈ ( − 2 ; − 1 ) ∪ ( 1 ; 2 ) .
Tập nghiệm của bất phương trình 2 x 2 − 4 − 1 . ln ( x 2 ) < 0 là
A. S = [ 1 ; 2 ] .
B. S = { 1 ; 2 } .
C. S = ( 1 ; 2 ) .
D. S = ( − 2 ; − 1 ) ∪ ( 1 ; 2 ) .
Cho hàm số f ( x ) = l n ( x 2 - 3 x ) . Tập nghiệm S của phương trình f'(x) = 0 là:
A. S = ∅
B. S = 3 2
C. S = {0;3}
D. S = - ∞ ; 0 ∪ 3 ; + ∞