Đáp án D
Ta có ln(2x2 + 3) > ln(x2 + ax + 1)
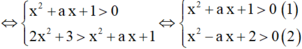
Giải (1), ta có x2 + ax + 1 > 0
∀ x ∈ ℝ ⇔ ∆ = a 2 - 4 < 0 ⇔ - 2 < a < 2 .
Giải (2), ta có x2 + ax + 2 > 0
∀ x ∈ ℝ ⇔ ∆ = - a 2 - 8 < 0 ⇔ - 2 2 < a < a 2 .
Vậy a thuộc (–2;2) là giá trị cần tìm.
Đáp án D
Ta có ln(2x2 + 3) > ln(x2 + ax + 1)
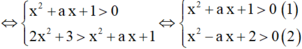
Giải (1), ta có x2 + ax + 1 > 0
∀ x ∈ ℝ ⇔ ∆ = a 2 - 4 < 0 ⇔ - 2 < a < 2 .
Giải (2), ta có x2 + ax + 2 > 0
∀ x ∈ ℝ ⇔ ∆ = - a 2 - 8 < 0 ⇔ - 2 2 < a < a 2 .
Vậy a thuộc (–2;2) là giá trị cần tìm.
Gọi a là số thực lớn nhất để bất phương trình x 2 - x + 2 + a ln ( x 2 - x + 1 ) ≥ 0 nghiệm đúng với mọi x. Mệnh đề nào sau đây đúng?
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Giải các bất phương trình sau:
a) (2x − 7)ln(x + 1) > 0;
b) (x − 5)(logx + 1) < 0;
c) 2 log 3 2 x + 5 log 2 2 x + log 2 x – 2 ≥ 0
d) ln(3 e x − 2) ≤ 2x
Cho phương trình m . l n 2 ( x + 1 ) - ( x + 2 - m ) l n ( x + 1 ) - x - 2 = 0 (1). Tập hợp tất cả các giá trị của tham số m để phương trình (1) có hai nghiệm phân biệt thoả mãn 0 < x 1 < 2 < 4 < x 2 là khoảng . Khi đó a thuộc khoảng
![]()
![]()
![]()
![]()
Tập nghiệm của bất phương trình 2 x 2 − 4 − 1 . ln ( x 2 ) < 0 là
A. S = [ 1 ; 2 ] .
B. S = { 1 ; 2 } .
C. S = ( 1 ; 2 ) .
D. S = ( − 2 ; − 1 ) ∪ ( 1 ; 2 ) .
Cho hàm số y = f ( x ) = ln ( 1 + x 2 + x ) .
Tập nghiệm của bất phương trình
f ( a - 1 ) + f ( ln a ) ≤ 0 là:
![]()
![]()
![]()
![]()
Số nghiệm của phương trình ln x + ln(3x – 2) = 0 là?
A. 1.
B. 3.
C. 0.
D. 2.
Cho hàm số f(x)=a x 2 -2(a+1)x+a+2 (a ≠ 0)
Chứng tỏ rằng phương trình f(x)=0 luôn có nghiệm thực. Tính các nghiệm đó.
Tìm tất cả các giá trị thực của tham số m sao cho mọi nghiệm của bất phương trình: x 2 - 3 x + 2 ≤ 0 cũng là nghiệm của bất phương trình m x 2 + ( m + 1 ) x + m + 1 ≥ 0 ?
A. m ≤ - 1 .
B. m ≤ - 4 7 .
C. m ≥ - 4 7 .
D. m ≥ - 1 .
Tìm tất cả các giá trị thực của tham số m sao cho mọi nghiệm của bất phương trình: x2-3x+2 ≤ 0 cũng là nghiệm của bất phương trình mx2+(m+1) x+m+1 ≥ 0
A. m ≤ - 1
B. m ≤ - 4 7
C. m ≥ - 4 7
D. m ≥ - 1