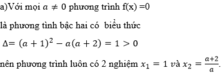Các câu hỏi tương tự
Cho hàm số f(x)=a x 2 -2(a+1)x+a+2 (a ≠ 0)
Tính tổng S và tích P của các nghiệm của phương trình f(x) =0. Khảo sát sự biến thiên và vẽ đồ thị của S và P theo a.
Cho hàm số
y
f
(
x
)
a
x
3
+
b
x
2
+
c
x
+
d
(
a
≠
0
)
có đồ thị như hình vẽ: Phương trình f(f(x))0 có bao nhiêu nghiệm thực? A. 3 B. 7 C. 9 D. 5
Đọc tiếp
Cho hàm số y = f ( x ) = a x 3 + b x 2 + c x + d ( a ≠ 0 ) có đồ thị như hình vẽ:
Phương trình f(f(x))=0 có bao nhiêu nghiệm thực?
A. 3
B. 7
C. 9
D. 5
Cho hàm số
f
(
x
)
-
1
3
x
3
+
2
x
2
-
3
x
+
1
. Khi đó phương trình f(f(x)) 0 có bao nhiêu nghiệm thực? A. 9 B. 6 C. 5 D. 4
Đọc tiếp
Cho hàm số f ( x ) = - 1 3 x 3 + 2 x 2 - 3 x + 1 . Khi đó phương trình f(f(x)) = 0 có bao nhiêu nghiệm thực?
A. 9
B. 6
C. 5
D. 4
Cho hàm số f(x) có bảng biến thiên như sau:
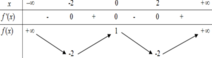
Số nghiệm thực của phương trình f(f(x)) + 2 = 0 là
A. 4
B. 3
C. 2
D. 6
Cho hàm số
y
f
(
x
)
ax
3
+
bx
2
+
cx
+
d
(
a
≠
0
)
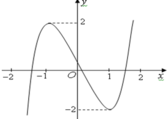
có đồ thị như hình vẽ. Phương trình f (f(x)) có bao nhiêu nghiệm thực? A. 5. B. 3. C. 7. D. 9.
Đọc tiếp
Cho hàm số y = f ( x ) = ax 3 + bx 2 + cx + d ( a ≠ 0 ) có đồ thị như hình vẽ. Phương trình f (f(x)) có bao nhiêu nghiệm thực?

A. 5.
B. 3.
C. 7.
D. 9.
Cho hàm số
f
(
x
)
a
x
4
+
b
x
2
-
1
(
a
,
b
∈
ℝ
)
. Đồ thị của hàm số yf(x) như hình vẽ bên. Số nghiệm thực của phương trình 2018.f(x) + 2019 0 là: A. 4 B. 0 C. 3 D. 2
Đọc tiếp
Cho hàm số f ( x ) = a x 4 + b x 2 - 1 ( a , b ∈ ℝ ) . Đồ thị của hàm số y=f(x) như hình vẽ bên. Số nghiệm thực của phương trình 2018.f(x) + 2019 = 0 là:
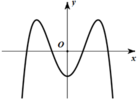
A. 4
B. 0
C. 3
D. 2
Cho hàm số y f (x) có bảng biến thiên như sau Số nghiệm thực của phương trình 2 f (x) + 3 0 là A. 4 B. 3 C. 2 D. 1
Đọc tiếp
Cho hàm số y = f (x) có bảng biến thiên như sau
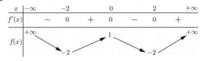
Số nghiệm thực của phương trình 2 f (x) + 3 = 0 là
A. 4
B. 3
C. 2
D. 1
Cho hàm số
f
(
x
)
a
x
4
+
b
x
2
(
a
,
b
∈
ℝ
)
có đồ thị hàm số f(x) như hình vẽ bên dưới. Biết rằng diện tích phần tô đậm bằng
1
8
. Phương trình 8f(x) + 1 0 có bao nhiêu nghiệm? A. 0 B. 4 C. 3...
Đọc tiếp
Cho hàm số f ( x ) = a x 4 + b x 2 ( a , b ∈ ℝ ) có đồ thị hàm số f'(x) như hình vẽ bên dưới. Biết rằng diện tích phần tô đậm bằng 1 8 . Phương trình 8f(x) + 1 = 0 có bao nhiêu nghiệm?
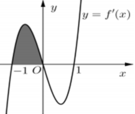
A. 0
B. 4
C. 3
D. 2
Người ta chứng tỏ rằng ở bậc n=6 các nghiệm của phương trình bậc n được biểu diễn như là sự chồng chất(superposition)các hàm liên tục có 2 biến của các hệ số của phương trình. Ví dụ các nghiệm của phương trình xX²+2Yx+z=0 được viết dưới dạng f(y,h(x,z) với h(x,z)=xz và f(y,u)=-y±√(y²-u). Kết quả này sẽ sai trong trường hợp n=7