Trong không gian Oxyz, cho hai mặt phẳng song song (P): 4x - 3y - 8 = 0 và (Q): 8x - 6y - 1 = 0. Khoảng cách giữa hai mặt phẳng (P) và (Q) là:
A. 15 100
B. 3 2
C. 15 101
D. 15 28
Trong không gian Oxyz, cho mặt phẳng ( P ) : x + 2 y + 2 z - 10 = 0 . Phương trình mặt phẳng (Q) song song với (P) và khoảng cách giữa hai mặt phẳng (P) và (Q) bằng 7 3 là
A. x + 2 y + 2 z - 3 = 0 ; x + 2 y + 2 z - 17 = 0
B. x + 2 y + 2 z + 3 = 0 ; x + 2 y + 2 z + 17 = 0
C. x + 2 y + 2 z + 3 = 0 ; x + 2 y + 2 z - 17 = 0
D. x + 2 y + 2 z - 3 = 0 ; x + 2 y + 2 z + 17 = 0
Trong không gian Oxyz, cho mặt phẳng (P): x+2y+2z-10 = 0. Phương trình mặt phẳng (Q) song song với (P) và khoảng cách giữa hai mặt phẳng (Q) và (P) bằng 7 3 là
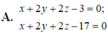
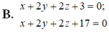
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng song song ( P ) : x − 2 y − 2 z + 1 = 0 và mặt phẳng ( Q ) : x − 2 y − 2 z − 2 = 0 . Khoảng cách h giữa hai mặt phẳng (P) và (Q) bằng bao nhiêu?
A. h = 1
B. h = 3
C. h = 1 3
D. h = 2 3
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): 3x-2y-z+5=0 và đường thẳng ∆ : x - 1 2 = y - 7 1 = z - 3 4 . Gọi (Q) là mặt phẳng chứa đường thẳng ∆ và song song với (P). Tính khoảng cách giữa hai mặt phẳng (P) và (Q).
A. 9 14
B. 9 14
C. 3 14
D. 3 14
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;2;3) và hai mặt phẳng (P): 2x+3y=0 và (Q): 3x+4y=0. Đường thẳng qua A song song với hai mặt phẳng (P); (Q) có phương trình tham số là:
A. x = t y = 2 z = 3 + t
B. x = 1 y = 1 z = 3
C. x = 1 + t y = 2 + t z = 3 + t
D. x = 1 y = 2 z = t
Đáp án D
Phương pháp :
Đường thẳng qua A song song với hai mặt phẳng (P); (Q) nhận ![]() là 1VTCP.
là 1VTCP.
Cách giải : Ta có ![]() lần lượt là các VTPT của
lần lượt là các VTPT của
Ta có :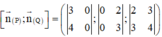
![]()
![]() là 1 VTCP của đường thẳng qua A và vuông góc với cả
là 1 VTCP của đường thẳng qua A và vuông góc với cả
Vậy phương trình đường thẳng cần tìm là: 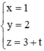
Với t = -3 ta có đường thẳng đi qua điểm B(1;2;0) => phương trình đường thẳng cần tìm là :
x = 1 y = 2 z = t
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;2;3) và hai mặt phẳng (P): 2x+3y=0 và (Q): 3x+4y=0. Đường thẳng qua A song song với hai mặt phẳng (P) và (Q) có phương trình tham số là:
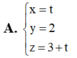
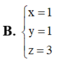
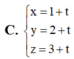
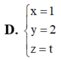
Đáp án D
Phương pháp :
Đường thẳng qua A song song với hai mặt phẳng (P), (Q)
![]()
Cách giải :
![]()
lần lượt là các VTPT của (P), (Q)
Ta có :
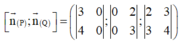
=(0;0;-1)
=> u → = ( 0 ; 0 ; 1 ) là 1 VTCP của đường thẳng qua A và vuông góc với cả (P), (Q)
Vậy phương trình đường thẳng cần tìm là:
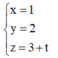
Với t =-3 ta có đường thẳng đi qua điểm B(1;2;0) =>phương trình đường thẳng cần tìm là :
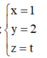
Trong không gian với hệ tọa độ Oxyz, cho điểm A 1 ; 2 ; 3 và hai mặt phẳng P : 2 x + 3 y = 0 , Q : 3 x + 4 y = 0 . Đường thẳng qua A song song với hai mặt phẳng P , Q có phương trình tham số là
A. x = 1 + t y = 2 + t z = 3 + t
B. x = 1 y = 2 z = t
C. x = t y = 2 z = 3 + t
D. x = 1 y = t z = 3
Trong không gian Oxyz, cho hai mặt phẳng P : x + 3 z + 2 = 0 , Q : x + 3 z - 4 = 0 . Mặt phẳng song song và cách đều P , Q có phương trình là
![]()
![]()
![]()
![]()
Trong không gian Oxyz, cho hai mặt phẳng P : x + 3 z + 2 = 0 , Q : x + 3 z - 4 = 0 . Mặt phẳng song song và cách đều (P), (Q) có phương trình là
A. x + 3 z - 2 = 0
B. x + 3z - 2 = 0
C. x + 3z - 1 = 0
D. x + 3z - 6 = 0