Đáp án B
Lấy một điểm M(2 ;0 ;0)∈(P). Vì hai mặt phẳng (P) và (Q) song song nên ta có:
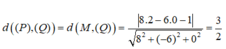
Đáp án B
Lấy một điểm M(2 ;0 ;0)∈(P). Vì hai mặt phẳng (P) và (Q) song song nên ta có:
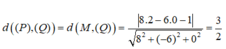
Trong không gian Oxyz, cho mặt phẳng (P): x+2y+2z-10 = 0. Phương trình mặt phẳng (Q) song song với (P) và khoảng cách giữa hai mặt phẳng (Q) và (P) bằng 7 3 là
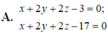
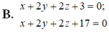
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): 3x-2y-z+5=0 và đường thẳng ∆ : x - 1 2 = y - 7 1 = z - 3 4 . Gọi (Q) là mặt phẳng chứa đường thẳng ∆ và song song với (P). Tính khoảng cách giữa hai mặt phẳng (P) và (Q).
A. 9 14
B. 9 14
C. 3 14
D. 3 14
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;2;3) và hai mặt phẳng (P): 2x+3y=0 và (Q): 3x+4y=0. Đường thẳng qua A song song với hai mặt phẳng (P) và (Q) có phương trình tham số là:
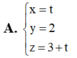
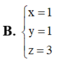
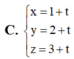
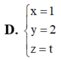
Trong không gian Oxyz, cho hai mặt phẳng P : x + 3 z + 2 = 0 , Q : x + 3 z - 4 = 0 . Mặt phẳng song song và cách đều P , Q có phương trình là
![]()
![]()
![]()
![]()
Trong không gian Oxyz, cho điểm A di động trên mặt phẳng (P): 2x - y - 2z = 0, điểm B di động trên mặt phẳng (Q): 4x - 2y - 4z - 9 = 0. Khoảng cách giữa hai điểm A và B nhỏ nhất là:
A. 3 2
B. 1 4
C. 9 28
D. 9 28
Trong không gian Oxyz, viết phương trình mặt phẳng (P) song song với mặt phẳng ( Q ) : x + 2 y - 2 z + 1 = 0 và cách (Q) một khoảng bằng 3.
A. x + 2 y - 2 z + 8 = 0 v à x + 2 y – 2 z – 10 = 0 .
B. x + 2 y - 2 z + 6 = 0 v à x + 2 y - 2 z – 8 = 0
C. x + 2 y – 2 z – 8 = 0 v à x + 2 y – 2 z + 10 = 0
D. Đáp án khác.
Trong không gian Oxyz, viết phương trình mặt phẳng (P) song song với mặt phẳng ( Q ) : x + 2 y - 2 z + 1 = 0 và cách (Q) một khoảng bằng 3.
A. x + 2 y - 2 z + 8 = 0 v à x + 2 y – 2 z – 10 = 0 .
B. x + 2 y - 2 z + 6 = 0 v à x + 2 y - 2 z – 8 = 0
C. x + 2 y – 2 z – 8 = 0 v à x + 2 y – 2 z + 10 = 0
D. Đáp án khác.
Trong không gian Oxyz, cho hai mặt phẳng (P): x + 2y - 2z - 6 = 0 và (Q): x + 2y - 2z + 3 = 0. Khoảng cách giữa hai mặt phẳng (P) và (Q) bằng
A. 3.
B. 6.
C. 1.
D. 9.
Trong không gian Oxyz, phương trình mặt phẳng (P) song song và cách mặt phẳng (Q): x+2y+2z-3=0 một khoảng bằng 1; đồng thời (P) không qua O là
![]()
![]()
![]()
![]()