Đáp án A
Khoảng cách nhỏ nhất giữa hai điểm A và B chính là khoảng cách giữa hai mặt phẳng (P) và (Q), dấu bằng xày ra khi và chỉ khi AB vuông góc với (P). Mặt khác vì O thuộc (P) nên ta có:
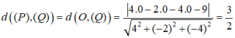
Vậy khoảng cách giữa hai điểm A và B nhỏ nhất bằng 3/2
Đáp án A
Khoảng cách nhỏ nhất giữa hai điểm A và B chính là khoảng cách giữa hai mặt phẳng (P) và (Q), dấu bằng xày ra khi và chỉ khi AB vuông góc với (P). Mặt khác vì O thuộc (P) nên ta có:
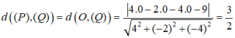
Vậy khoảng cách giữa hai điểm A và B nhỏ nhất bằng 3/2
Trong không gian Oxyz cho mặt cầu (S): (x-1)²+ (y-2)²+ (z-3)²=9 và mặt phẳng (P): 2x-2y+z+3=0. Gọi M (a;b;c) là điểm trên mặt cầu sao cho khoảng cách từ M đến (P) lớn nhất. Khi đó:
A. a+b+c=8.
B. a+b+c=5.
C. a+b+c=6.
D. a+b+c=7.
Trong không gian Oxyz, cho mặt cầu (S): x - 1 2 + y - 1 2 + z - 1 2 = 12 và mặt phẳng (P): x-2y+2z+11=0. Xét điểm M di động trên (P); các điểm A, B, C phân biệt di động trên (S) sao cho AM, BM, CM là các tiếp tuyến của (S). Mặt phẳng (ABC) luôn đi qua điểm cố định nào dưới đây?
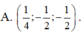
![]()
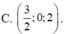
![]()
Trong không gian với hệ tọa độ Oxyz, cho điểm A(-2;1;5) và hai mặt phẳng (P): 2x + y + 3z - 7 = 0, (Q): 3x - 2y - z + 1 = 0. Gọi M là điểm nằm trên mặt phẳng (P) và điểm N nằm trên mặt phẳng (Q) thỏa mãn A M → = 2 A N → . Khi M di động trên mặt phẳng (P) thì quỹ tích điểm N là một đường thẳng có phương trình là
A. x = - 3 - 5 t y = - 1 + 11 t z = 6 - 7 t
B. x = 1 + 7 t y = - 8 - 5 t z = 6 - 7 t
C. x = 7 + 11 t y = - 8 - 5 t z = - 8 - 7 t
D. x = 2 + 5 t y = 3 + 11 t z = - 1 - 7 t
Trong không gian Oxyz, cho điểm A(1;2;-3) mặt phẳng (P): 2x+2y-z+9=0 và đường thẳng ∆ : x + 1 3 = y 4 = z + 2 - 4 Đường thẳng d đi qua A, song song với ∆ và cắt tại B. Điểm M di động trên (P) sao cho tam giác AMB luôn vuông tại M. Độ dài đoạn MB có giá trị lớn nhất bằng
![]()
![]()
![]()
![]()
Trong không gian Oxyz, cho hai điểm A(10;6;-2), B(5;10;-9) và mặt phẳng ( α ) : 2 x + 2 y + z - 12 = 0 Điểm M di động trên mặt phẳng ( α ) sao cho MA, MB luôn tạo với ( α ) các góc bằng nhau. Biết rằng M luôn thuộc một đường tròn ( ω ) cố định. Hoành độ của tâm đường tròn ( ω ) bằng
A. 9 2
B. 2
C. 10
D. -4
Trong không gian Oxyz, cho mặt cầu S : x 2 + y 2 + z 2 − 4 x + 2 y − 6 z + 5 = 0 và mặt phẳng P : 2 x + 2 y − z + 16 = 0 . Điểm M, N di động lần lượt trên (S) và (P). Khi đó giá trị nhỏ nhất của đoạn MN là
A. 8
B. 3
C. 2
D. 5
Trong không gian Oxyz, cho mặt cầu (S): ( x + 1 ) 2 + ( y - 1 ) 2 + ( z - 2 ) 2 = 9 và mặt phẳng (P): 2x-2y+z+14=0. Gọi M ( a ; b ; c ) là điểm thuộc mặt cầu (S) sao cho khoảng cách từ M đến mặt phẳng (P) lớn nhất. Tính T = a + b + c .
![]()
![]()
![]()
![]()
Trong không gian Oxyz cho ba điểm A(-10;-5;8), B(2;1;-1), C(2;3;0) và mặt phẳng (P): x+2y-2z-9=0. Xét điểm M là điểm thay đổi trên (P) sao cho M A 2 + 2 M B 2 + 3 M C 2 đạt giá trị nhỏ nhất. Tính M A 2 + 2 M B 2 + 3 M C 2
A. 54
B. 282
C. 256
D. 328
Trong không gian Oxyz, cho hai mặt phẳng (P): x + 2y - 2z + 1 = 0, (Q): 2x + 4y + az + b = 0. Tìm a và b sao cho khoảng cách giữa hai mặt phẳng đó bằng 1.
A. a=-4 và b=8
B. a=-4 và b=8 hoặc b=-4
C. a=-2 và b=38 hoặc b=-34
D. a=-4 và b=38 hoặc b=-34