Tìm số phức Z, biết Z là nghiệm của phương trình: ( 2 i - 1 ) Z 2 - 2 i Z ¯ + ( 6 + 4 i ) = 0
A. Z = -i
B. Z = 1-i
C. Z = 1+i
D. Z = i
Số nghiệm phức của phương trình z + 2 | z | + 3 - i = ( 4 + i ) | z | z là
A. 1.
B. 2.
C. 3.
D. 4.
Số phức z nào dưới đây là nghiệm phương trình (1+i) z 2 - ( 2 - i ) z ¯ + i - 2 = 0 ?
A. z = 4
B. z = 1 + i
C. z = -2i
D. z = 2 - i
Số phức z=a+bi, a,b thuộc R là nghiệm của phương trình ( z - 1 ) ( 1 + i z z - 1 z = i . Tổng T=a^2+b^2 bằng
A. ![]() .
.
B. ![]() .
.
C.![]()
D. ![]() .
.
Số phức z nào dưới đây là nghiệm của phương trình: ( - 1 + i ) z 4 - 3 ( 2 - i ) z 2 + ( 16 i + 2 ) = 0
A. z = i
B. z = -i
C. z = i + 1
D. z = 5
Số nghiệm của phương trình với ẩn số phức z: 4z2 + 8|z|2 - 3 = 0 là:
A. 3.
B. 2.
C. 4.
D. 1.
Chọn C.
Gọi z = a + bi là nghiệm của phương trình.
Ta có: 4(a + bi) 2 + 8(a2 + b2) - 3 = 0
4(a2 – b2 + 2abi) + 8( a2 + b2) - 3 = 0
12a2 + 4b2 +8abi - 3 = 0
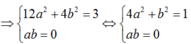
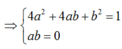

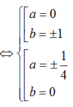
Vậy phương trình có 4 nghiệm phức.
Gọi z1; z2; z3; z4 là bốn nghiệm của phương trình ( z - 1 )( z + 2) ( z2 - 2z + 2) = 0 trên tập số phức, tính tổng: 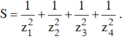
A. 2/5
B. 3/5
C. 5/4
D. 6/7
Chọn C.
Không mất tính tổng quát ta gọi 4 nghiệm của phương trình là:
z1= 1; z2= - 2; z3= 1+ i và z4 = 1 - i
Thay vào biểu thức
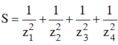
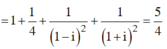
Cho số phức thỏa mãn z - i = z - 1 + 2 i . Tập hợp điểm biểu diễn số phức w = (2 - i) z +1 trên mặt phẳng phức là một đường thẳng. Phương trình của đường thẳng đó là
![]()
![]()
![]()
![]()
Số phức thỏa mãn phương trình z + 3 z ¯ = ( 2 + i ) 3 ( 2 - i ) Mô đun của số phức w = z + 10 i là
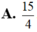
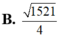
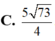
![]()
Số phức thỏa mãn phương trình z + 3 z = 2 + i 3 ( 2 - i ) Mô đun của số phức w = z + 10i là
A. 15 4
B. 1521 4
C. 5 73 4
D. 4