Cho tứ diện ABCD có ABCD3, ADBC5, ACBD6. Tính thể tích khối cầu ngoại tiếp tứ diện ABCD.
Đọc tiếp
Cho tứ diện ABCD có AB=CD=3, AD=BC=5, AC=BD=6. Tính thể tích khối cầu ngoại tiếp tứ diện ABCD.
Những câu hỏi liên quan
Cho tứ diện ABCD có ABBCCD2, ACBD1, AD
3
. Tính bán kính của mặt cầu ngoại tiếp tứ diện đã cho.
Đọc tiếp
Cho tứ diện ABCD có AB=BC=CD=2, AC=BD=1, AD= 3 . Tính bán kính của mặt cầu ngoại tiếp tứ diện đã cho.
Cho tứ diện ABCD có AB BC CD 2, AC BD 1, AD
3
. Tính bán kính của mặt cầu ngoại tiếp tứ diện đã cho.
Đọc tiếp
Cho tứ diện ABCD có AB = BC = CD = 2, AC = BD = 1, AD = 3 . Tính bán kính của mặt cầu ngoại tiếp tứ diện đã cho.
Cho tứ diện ABCD có AB CD x, AC BD y,
A
D
B
C
2
3
. Bán kính khối cầu ngoại tiếp tứ diện ABCD bằng
2
. Giá trị lớn nhất của xy bằng A. 2. B. 4. C.
2
2
D.
2
Đọc tiếp
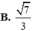
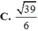
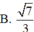
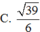
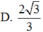
Cho tứ diện ABCD có AB =CD =x, AC =BD =y, A D = B C = 2 3 . Bán kính khối cầu ngoại tiếp tứ diện ABCD bằng 2 . Giá trị lớn nhất của xy bằng
A. 2.
B. 4.
C. 2 2
D. 2
Cho tứ diện ABCD có BC 3, CD 4,
B
C
D
⏜
A
B
C
⏜
A
D
C
⏜
90
°
. Góc giữa hai đường thẳng AD và BC bằng
60
°
. Tính thể tích khối cầu ngoại tiếp tứ diện ABCD A. ...
Đọc tiếp
Cho tứ diện ABCD có BC = 3, CD = 4, B C D ⏜ = A B C ⏜ = A D C ⏜ = 90 ° . Góc giữa hai đường thẳng AD và BC bằng 60 ° . Tính thể tích khối cầu ngoại tiếp tứ diện ABCD
A. 127 127 π 6
B. 52 13 π 3
C. 28 7 π 3
D. 32 3 π
Cho tứ diện ABCD có BC 3, CD 4,
BCD
^
ABC
^
ADC
^
90
o
. Góc giữa hai đường thẳng AB và CD bằng...
Đọc tiếp
Cho tứ diện ABCD có BC = 3, CD = 4, BCD ^ = ABC ^ = ADC ^ = 90 o . Góc giữa hai đường thẳng AB và CD bằng 60 o Tính thể tích khối cầu ngoại tiếp tứ diện ABCD
A. 127 127 π 6
B. 52 13 π 3
C. 28 7 π 3
D. 16 12 π
Cho tứ diện ABCD có
A
B
C
D
11
m
;
B
C
A
D
20
m
;
B
D
A
C
21
m
. Tính thể tích khối tứ diện ABCD. A. 770
m
3
B. 340
m
3
C. 720
m
3
D. 3...
Đọc tiếp
Cho tứ diện ABCD có A B = C D = 11 m ; B C = A D = 20 m ; B D = A C = 21 m . Tính thể tích khối tứ diện ABCD.
A. 770 m 3
B. 340 m 3
C. 720 m 3
D. 360 m 3
Phương pháp:
Dựng hình hộp chữ nhật AMCN.PBQD sao cho các đường chéo A B = C D = 11 m ; B C = A D = 20 m ; B D = A C = 21 m
Từ đó ta phân chia thể tích các hình chóp nhỏ trong hình hộp chữ nhật để tính được V A B C D theo thể tích hình hộp chữ nhật.
Dựa vào định lý Pytago để tính các kích thước của hình hộp chữ nhật từ đó suy ra thể tích V A B C D
Cách giải:
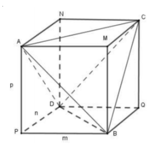
Dựng hình hộp chữ nhật AMCN.PBQD như hình bên. Khi đó
Tứ diện ABCD thỏa mãn A B = C D = 11 m ; B C = A D = 20 m ; B D = A C = 21 m
Gọi các kích thước hình hộp chữ nhật là m; n; p. Gọi
Đúng 0
Bình luận (0)
Cho tứ diện ABCD có
A
B
a
2
,
A
C
A
D
a
,
B
C
B
D
a
,
C
D
a
. Tính thể tích V của khối tứ diện ABCD. A.
V
a
3
2...
Đọc tiếp
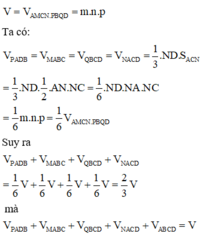
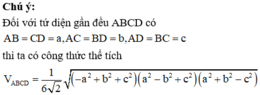
Cho tứ diện ABCD có A B = a 2 , A C = A D = a , B C = B D = a , C D = a . Tính thể tích V của khối tứ diện ABCD.
A. V = a 3 2 12
B. V = a 3 6 8
C. V = a 3 6 24
D. V = a 3 2 4
Chọn A
Gọi H là hình chiếu vuông góc của A trên (BCD). Khi đó CD vuông góc với mp(ABH).
Thể tích tứ diện ABCD gấp đôi thể tích của tứ diện ABCE, với E là trung điểm CD.
Cách khác: Gọi I là trung điểm AB.
Dễ thấy IACD và IBCD là các tứ diện vuông tại I, có các cạnh góc vuông là a 2
Đúng 0
Bình luận (0)
Cho tứ diện ABCD có
A
B
a
2
, ACADa, BCBDa, CDa. Tính thể tích V của khối tứ diện ABCD.
Đọc tiếp
Cho tứ diện ABCD có A B = a 2 , AC=AD=a, BC=BD=a, CD=a. Tính thể tích V của khối tứ diện ABCD.
Cho tứ diện ABCD có ABBCACBD2a, AD
a
3
; hai mặt phẳng (ACD) và (BCD) vuông góc với nhau. Diện tích mặt cầu ngoại tiếp tứ diện ABCD bằng
Đọc tiếp
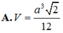
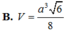
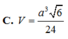
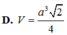
Cho tứ diện ABCD có AB=BC=AC=BD=2a, AD= a 3 ; hai mặt phẳng (ACD) và (BCD) vuông góc với nhau. Diện tích mặt cầu ngoại tiếp tứ diện ABCD bằng
