Cho khối tứ diện ABCD có thể tích V. Gọi G 1 , G 2 , G 3 , G 4 là trọng tâm 4 mặt của tứ diện ABCD. Thể tích của khối tứ diện G 1 G 2 G 3 G 4 là
A. V 27
B. V 18
C. V 4
D. V 12
Đáp án A
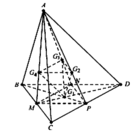
Ta có d G 1 ; G 2 G 3 G 4 = 1 2 d A ; G 2 G 3 G 4
= 1 2 . 2 3 d A ; M N P = 1 3 d A ; M N P S G 2 G 3 G 4 = 2 3 2 S M N P = 4 9 . 1 4 S A B C = 1 9 S A B C
Thể tích của khối tứ diện G 1 G 2 G 3 G 4 là
V = 1 3 d G 1 ; G 2 G 3 G 4 . S G 2 G 3 G 4 = 1 3 . 1 3 . d A ; M N P . 1 9 S A B C = 1 27 V A B C D = V 27
Cho tứ diện ABCD có thể tích V . Gọi M, N, P, Q lần lượt là trọng tâm tam giác ABC, ACD, ABD và BCD . Thể tích khối tứ diện MNPQ bằng
A. 4 V 9
B. V 27
C. V 9
D. 4 V 27
Cho khối tứ diện ABCD có thể tích V. Gọi G 1 , G 2 , G 3 , G 4 là trọng tâm 4 mặt của tứ diện ABCD. Thể tích của khối tứ diện G 1 , G 2 , G 3 , G 4 là
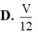
Cho khối tứ diện ABCD có thể tích V. Gọi G 1 G 2 G 3 G 4 là trọng tâm của 4 mặt của tứ diện ABCD. Thể tích của khối tứ diện G 1 G 2 G 3 G 4 là
A. V 27
B. V 18
C. V 4
D. V 12
Cho khối tứ diện ABCD có thể tích V. Gọi G 1 , G 2 , G 3 , G 4 là trọng tâm của 4 mặt của tứ diện ABCD. Thể tích của khối tứ diện G 1 , G 2 , G 3 , G 4 là
A. V/27
B. V/18
C. V/4
D. V/12
Đáp án A
Ta có d G 1 ; G 2 G 3 G 4 = 1 2 d A ; G 2 G 3 G 4
= 1 2 . 2 3 d A ; M N P = 1 3 d A ; M N P
S G 2 G 3 G 4 = 2 3 2 S M N P = 4 9 . 1 4 S A B C = 1 9 S A B C
Thể tích của khối tứ diện G 1 G 2 G 3 G 4 là
V = 1 3 d G 1 ; G 2 G 3 G 4 . S G 2 G 3 G 4 = 1 3 . 1 3 d A ; M N P . 1 9 S A B C
= 1 27 V A B C D = V 27
Cho tứ diện ABCD có thể tích 9 3 c m 3 . Gọi M, N, P, Q lần lượt là trọng tâm các mặt của khối tứ diện ABCD . Thể tích khối tứ diện MNPQ là
A. 2 3 3 c m 3
B. 3 3 c m 3
C. 3 3 c m 3
D. 3 c m 3
Đáp án B
Ta có:
V M N P Q V A B C D = 1 3 . 1 3 2 = 1 27 ⇒ V M N P Q = V A B C D 27 = 9 3 27 = 3 3 c m 3
Cho khối tứ diện ABCD có thể tích 2017. Gọi M, N, P, Q lần lượt là trọng tâm của các tam giác ABC, ABD, ACD, BCD. Tính theo V thể tích của khối tứ diện MNPQ.
A. 2017 9
B. 4034 81
C. 8068 27
D. 2017 27
Chọn D
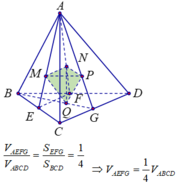
(Do E, F, G lần lượt là trung điểm của BC, BD, CD).
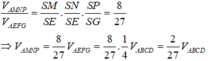
Do mặt phẳng (MNP) (BCD) nên
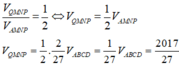
Cho tứ diện ABCD có AB=3a, AC=4a,AD=5a. Gọi M,N,P lần lượt là trọng tâm các tam giác DAB, DBC,DCA. Tính thể tích V của tứ diện DMNP khi thể tích tứ diện BACD đạt giá trị lớn nhất.
A. V = 120 a 3 27
B. V + 10 a 3 4
C. V = 80 a 3 7
D. V = 20 a 3 27
Cho khối tứ diện ABCD có thể tích là V. Gọi E, F, G lần lượt là trung điểm BC, BD, CD và M, N, P, Q lần lượt là trọng tâm ∆ A B C ; ∆ A B D ; ∆ A C D ; ∆ B C D . Tính thể tích khối tứ diện MNPQ theo V.
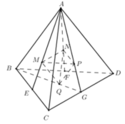
A. V 9
B. V 3
C. 2 V 9
D. V 27
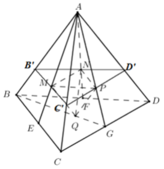
Ta có:
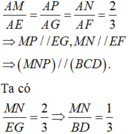
Ta có ∆ M N P đồng dạng với ∆ B C D theo tỉ số
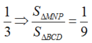
Dựng B ' C ' qua M và song song BC. C ' D ' qua P và song song với CD.
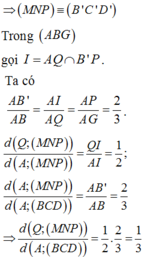
Chọn D.
