Các câu hỏi tương tự
Cho tứ diện ABCD có các cạnh AB, AC, AD đôi một vuông góc với nhau; AB 3a, AC 4a, AD 5a. Gọi M, N, P lần lượt là trọng tâm của tam giác DAB, DBC, DCA. Tính thể tích của khối chóp DMNA theo a. A.
V
10
a
3
27
B.
V
80
a
3
27
C....
Đọc tiếp
Cho tứ diện ABCD có các cạnh AB, AC, AD đôi một vuông góc với nhau; AB = 3a, AC = 4a, AD = 5a. Gọi M, N, P lần lượt là trọng tâm của tam giác DAB, DBC, DCA. Tính thể tích của khối chóp DMNA theo a.
A. V = 10 a 3 27
B. V = 80 a 3 27
C. V = 20 a 3 27
D. V = 40 a 3 27
Cho tứ diện ABCD có thể tích V. Gọi
A
1
B
1
C
1
D
1
là tứ diện với các đỉnh lần lượt là trọng tâm tam giác BCD, CDA, DAB, ABC và có thể tích
V
1
. Gọi
A
2
B
2
C
2
D
2...
Đọc tiếp
Cho tứ diện ABCD có thể tích V. Gọi A 1 B 1 C 1 D 1 là tứ diện với các đỉnh lần lượt là trọng tâm tam giác BCD, CDA, DAB, ABC và có thể tích V 1 . Gọi A 2 B 2 C 2 D 2 là tứ diện với các đỉnh lần lượt là trọng tâm tam giác B 1 C 1 D 1 , C 1 D 1 A 1 , D 1 A 1 B 1 , A 1 B 1 C 1 và có thể tích V 2 … cứ như vậy cho tứ diện A n B n C n D n có thể tích V n với n là số tự nhiên lớn hơn 1. Tính giá trị của biểu thức P = lim n → + ∞ V + V 1 + ... + V n .
A. 27 26 V
B. 1 27 V
C. 9 8 V
D. 82 81 V
Cho khối tứ diện ADCD có thể tích V. Gọi M, N, P, Q lần lượt là trọng tâm của các tam giác ABC, ABD, ACD, BCD. Tính theo V thể tích của khối tứ diện MNPQ. A.
V
27
B.
4
V
27
C.
2
V
81
D.
V
9
Đọc tiếp
Cho khối tứ diện ADCD có thể tích V. Gọi M, N, P, Q lần lượt là trọng tâm của các tam giác ABC, ABD, ACD, BCD. Tính theo V thể tích của khối tứ diện MNPQ.
A. V 27
B. 4 V 27
C. 2 V 81
D. V 9
Cho tứ diện ABCD có thể tích V . Gọi M;N;P;Q lần lượt là trọng tâm tam giác
A
B
C
,
A
C
D
,
A
B
D
và BCD . Thể tích khối tứ diện MNPQ bằng: A. 4V/9 B. V/27 C. V/9 D. 4V/27
Đọc tiếp
Cho tứ diện ABCD có thể tích V . Gọi M;N;P;Q lần lượt là trọng tâm tam giác A B C , A C D , A B D và BCD . Thể tích khối tứ diện MNPQ bằng:
A. 4V/9
B. V/27
C. V/9
D. 4V/27
Cho tứ diện ABCD có thể tích là V. Điểm M thay đổi trong tam giác BCD Các đường thẳng qua M và song song với
A
B
,
A
C
,
A
D
lần lượt cắt các mặt phẳng
A
C
D
,
A
B
D
,
A
B
C
tại N;P;Q. Giá trị l...
Đọc tiếp
Cho tứ diện ABCD có thể tích là V. Điểm M thay đổi trong tam giác BCD Các đường thẳng qua M và song song với A B , A C , A D lần lượt cắt các mặt phẳng A C D , A B D , A B C tại N;P;Q. Giá trị lớn nhất của thể tích khối đa diện MNPQ là
A. V/27
B. V/16
C. V/8
D. V/18
Cho tứ diện đều ABCD có cạnh bằng 3. Gọi M, N lần lượt là trung điểm các cạnh AD, BD. Gọi P là điểm trên cạnh AB sao cho
P
B
P
A
2018
2017
. Tính thể tích V của khối tứ diện PMNC. A.
27.
2
12
B.
9.2018....
Đọc tiếp
Cho tứ diện đều ABCD có cạnh bằng 3. Gọi M, N lần lượt là trung điểm các cạnh AD, BD. Gọi P là điểm trên cạnh AB sao cho P B P A = 2018 2017 . Tính thể tích V của khối tứ diện PMNC.
A. 27. 2 12
B. 9.2018. 2 16.2017
C. 9. 2 16
D. 9.2017. 2 16.2018
Cho tứ diện ABCD có các cạnh AB, AC và AD đôi một vuông góc với nhau,
A
B
6
a
,
A
C
5
a
,
A
D
4
a
.
Gọi M, N, P tương ứng là trung điểm của các cạnh BC, CD, DB. Thể tích V của tứ diện AMNP là: A.
V
5...
Đọc tiếp
Cho tứ diện ABCD có các cạnh AB, AC và AD đôi một vuông góc với nhau, A B = 6 a , A C = 5 a , A D = 4 a . Gọi M, N, P tương ứng là trung điểm của các cạnh BC, CD, DB. Thể tích V của tứ diện AMNP là:
A. V = 5 a 3 3 .
B. V = 20 a 3 3 .
C. V = 5 a 3
D. V = 10 a 3
Cho khối tứ diện ABCD có thể tích là V. Gọi E, F, G lần lượt là trung điểm BC, BD, CD và M, N, P, Q lần lượt là trọng tâm
∆
A
B
C
;
∆
A
B
D
;
∆
A
C
D
;
∆
B
C
D
. Tính thể tích khối tứ diện MNPQ theo V. A.
V
9
B.
V
3
C. ...
Đọc tiếp
Cho khối tứ diện ABCD có thể tích là V. Gọi E, F, G lần lượt là trung điểm BC, BD, CD và M, N, P, Q lần lượt là trọng tâm ∆ A B C ; ∆ A B D ; ∆ A C D ; ∆ B C D . Tính thể tích khối tứ diện MNPQ theo V.
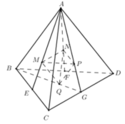
A. V 9
B. V 3
C. 2 V 9
D. V 27
Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB, BC và E là điểm đối xứng với B qua D. Mặt phẳng (MNE) chia khối tứ diện ABCD thành hai khối đa diện, trong đó khối chứa điểm A có thể tích V. Tính V A.
11
2
a
3
216
B.
7...
Đọc tiếp
Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB, BC và E là điểm đối xứng với B qua D. Mặt phẳng (MNE) chia khối tứ diện ABCD thành hai khối đa diện, trong đó khối chứa điểm A có thể tích V. Tính V
A. 11 2 a 3 216
B. 7 2 a 3 216
C. 2 a 3 8
D. 13 2 a 3 216