Cho hàm số y=ax3+bx2+cx+d có hai điểm cực trị x1, x2 thỏa mãn x 1 ∈ - 3 ; - 1 ; x 2 ∈ 0 ; 1 . Biết hàm số nghịch biến trên khoảng (x1, x2) và đồ thị hàm số cắt trục tung tại điểm có tung độ dương. Mệnh đề nào dưới đây là đúng?
![]()
![]()
![]()
![]()
Cho hàm số y = f x = a x 3 + b x 2 + c x + d có hai cực trị x 1 , x 2 thỏa mãn - 2 < x 1 < 0 < x 2 < 2 và có đồ thị như hình vẽ.
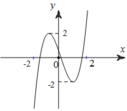
Số điểm cực tiểu của hàm số y = f(x) là
A. 3.
B. 5.
C. 7.
D. 4.
Cho hàm số y = f ( x ) = ax 3 + bx 2 + cx + d có hai cực trị x 1 , x 2 thỏa - 2 < x 1 < 0 < x 2 < 2 và có đồ thị như hình vẽ.
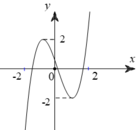
Số điểm cực tiểu của hàm số ![]() là
là
A. 3.
B. 5.
C. 7.
D. 4.

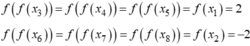
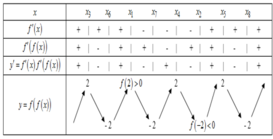
Suy ra số điểm cực tiểu của hàm số ![]() là 4
là 4
Cho hàm số y = a x 3 + b x 2 + c x + d đạt cực trị tại các điểm x 1 , x 2 thỏa mãn x 1 ∈ - 1 ; 0 , x 2 ∈ 1 ; 2 . Biết hàm số đồng biến trên ( x 1 , x 2 ). Đồ thị hàm số cắt trục tung tại điểm có tung độ âm. Trong các khẳng định sau, khẳng định nào đúng?
A. a < 0 , b > 0 , c > 0 , d < 0
B. a < 0 , b < 0 , c > 0 , d < 0
C. a > 0 , b > 0 , c > 0 , d < 0
D. a < 0 , b > 0 , c < 0 , d < 0
Đáp án A
Đồ thị cắt trục tung tại điểm có tung độ âm ⇒ y 0 = d < 0
Ta có y ' = 3 a x 2 + 3 b x + c , y ' = 0 ⇔ x 1 + x 2 = - 2 b 3 a x 1 . x 2 = c 3 a . Mà y ' > 0 , ∀ x ∈ x 1 , x 2 ⇒ a < 0
Mặt khác x 1 + x 2 > 0 x 1 . x 2 < 0 ⇒ - 2 b 3 a > 0 c 3 a < 0 ⇔ b > 0 c < 0 . Vậy a < 0 , b > 0 , c > 0 , d < 0 .
Cho hàm số y = a x 3 + b x 2 + c x + d đạt cực trị tại các điểm x 1 , x 2 thỏa mãn x 1 ∈ - 1 ; 0 ; x 2 ∈ 1 ; 2 . Biết hàm số đồng biến trên khoảng x 1 ; x 2 . Đồ thị hàm số cắt trục tung tại điểm có tung độ âm. Trong các khẳng định sau, khẳng định nào đúng?
A. a < 0 , b > 0 , c > 0 , d < 0
B. a < 0 , b < 0 , c > 0 , d < 0
C. a < 0 , b < 0 , c < 0 , d < 0
D. a < 0 , b > 0 , c < 0 , d < 0
Cho hàm số y = a x 3 + b x 2 + c x + d a ≠ 0 đạt cực trị tại các điểm x 1 , x 2 thỏa mãn x 1 ∈ - 1 ; 0 , x 2 ∈ 1 ; 2 . Biết hàm số đồng biến trên khoảng x 1 ; x 2 , đồ thị hàm số cắt trục tung tại điểm có tung độ dương. Khẳng định nào dưới đây đúng?
A. a < 0 , b > 0 , c > 0 , d > 0
B. a < 0 , b < 0 , c > 0 , d > 0
C. a > 0 , b > 0 , c > 0 , d > 0
D. a < 0 , b > 0 , c < 0 , d > 0
Chọn đáp án A.
Đồ thị hàm số cắt trục tung tại điểm có tung độ dương nên d > 0
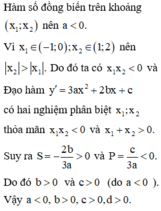

Hàm số y = a x 3 + b x 2 + c x + d đạt cực trị tại x 1 , x 2 nằm về hai phía của đường thẳng x = 3 khi
A. c + 6b < -27a
B. a và c trái dấu
C. c + 6 b 3 a < - 9
D. Đáp án khác
y = a x 3 + b x 2 + c x + d ⇒ y ' = 3 a x 2 + 2 b x + c
Hai cực trị tại x 1 , x 2 nằm về hai phía của đường thẳng x = 3 khi x 1 < 3 < x 2
⇒ 3 a f 3 < 0 ⇔ 3 a 27 a + 6 b + c < 0 ⇔ a 6 b + c < - 27 a 2 ⇔ 6 b + c 3 a < - 9
Đáp án cần chọn là C
Hàm số y = ax 3 + b x 2 + c x + d đạt cực trị tại x 1 , x 2 nằm về hai phía của đường thẳng x = 3 khi.
A. c + 6b < - 27a
B. a và c trái dấu
C. c + 6 b 3 a < - 9
D. Đáp án khác
Cho hàm số y = a x 3 + b x 2 + c x + d có đồ thị nhận hai điểm A(0;3) và B(2;-1) làm hai điểm cực trị. Số điểm cực trị của đồ thị hàm số y = a x 2 x + b x 2 + c x + d là:
A. 7
B. 5
C. 9
D. 11
Cho hàm số bậc ba y = ax 3 + bx 2 + cx + d có đồ thị nhận hai điểm A(0;3) và B(2;-1) làm hai điểm cực trị. Khi đó số điểm cực trị của hàm số y = | ax 2 | x | + bx 2 + c | x | + d | là
A. 5
B. 7
C. 9
D. 11