Cho hình chóp đều S.ABCD có cạnh đáy bằng 2a và cạnh bên bằng a 5 . Gọi (P) là mặt phẳng đi qua A và vuông góc với SC. Gọi β là góc tạo bởi mp (P) và (ABCD). Tính tan β
A. tan β = 6 3
B. tan β = 6 2
C. tan β = 2 3
D. tan β = 3 2
Cho hình chóp đều S.ABCD có cạnh đáy bằng 2a và cạnh bên bằng a 5 . Gọi (P) là mặt phẳng đi qua A và vuông góc với SC. Gọi β là góc tạo bởi mp (P) và (ABCD). Tính tan β
A. tan β = 6 3
B. tan β = 6 2
C. tan β = 2 3
D. tan β = 3 2
Phương pháp:
Sử dụng lý thuyết: Góc giữa hai mặt phẳng bằng góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng ấy.
Cách giải:

Gọi O là tâm hình vuông ABCD.
Ta có: 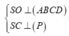
=> góc giữa (ABCD) và (P) là góc giữa SC và SO hay SCO.
Hình vuông ABCD cạnh 2a nên ![]()
Tam giác SOC vuông tại O nên
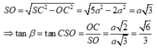
Chọn: A
Cho hình chóp đều S.ABCD có cạnh đáy bằng 2a và cạnh bên bằng a 5 . Gọi (P) là mặt phẳng đi qua A và vuông góc với SC. Gọi β là góc tạo bởi mp (P) và (ABCD). Tính tan β
![]()
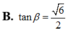
![]()
![]()
Cho khối chóp tứ giác đều S.ABCD, gọi α mặt phẳng qua A và vuông góc SC.
Biết rằng diện tích thiết diện tạo bởi α là hình chóp bằng nửa diện tích đáy ABCD. Tính
góc φ tạo bởi cạnh bên SC và mặt đáy.
A. φ = arcsin 1 + 33 8
B. φ = arcsin 33 − 1 8
C. φ = arcsin 1 + 29 8
D. φ = arcsin 29 − 1 8
Cho khối chóp tứ giác đều S.ABCD, gọi α mặt phẳng qua A và vuông góc SC. Biết rằng diện tích thiết diện tạo bởi α là hình chóp bằng nửa diện tích đáy ABCD. Tính góc φ tạo bởi cạnh bên SC và mặt đáy.
A. φ = a r c sin 33 + 1 8
B. φ = a r c sin 33 - 1 8
C. φ = a r c sin 29 + 1 8
D. φ = a r c sin 29 - 1 8
Đáp án A
Đặt a> 0 cạnh hình vuông là Dễ thấy
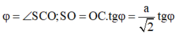
Gọi O là tâm của đáy. Vẽ AH ⊥ SC tại, H, AH cắt SO tại I thì A I O ^ = φ
![]()
Qua I vẽ đường thẳng song song DB cắt SD, SB theo thứ tự tại K, L. Thiết diện chính là tứ giác
ALHK và tứ giác này có hai đường chéo AH ⊥ KL Suy ra
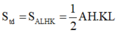
Ta có:


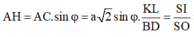
![]()
Theo giả thiết
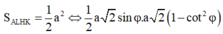
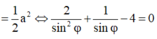
Giải được
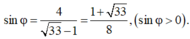
Suy ra φ = a r c sin 33 + 1 8
Cho hình chóp \(S.ABCD\) có độ dài cạnh đáy là \(a\). Gọi \(O\) là giao điểm của \(AC\) và \(BD\).
Độ dài các cạnh bên là \(a\sqrt{2}\). Măt phẳng mp(P) là mặt phẳng đi qua \(BD\) và vuông góc với \(SC\). Tính \(Cotg\) của góc tạo bởi đường thẳng \(AB\) và \(mp\left(P\right)\) là bao nhiêu ?
P/s: Trường THPT Phan Huy Chú ,thành phố Hà Nội
Em xin phép nhờ quý thầy cô giáo và các bạn yêu toán gợi ý giúp đỡ em với ạ
Em cám ơn nhiều lắm ạ!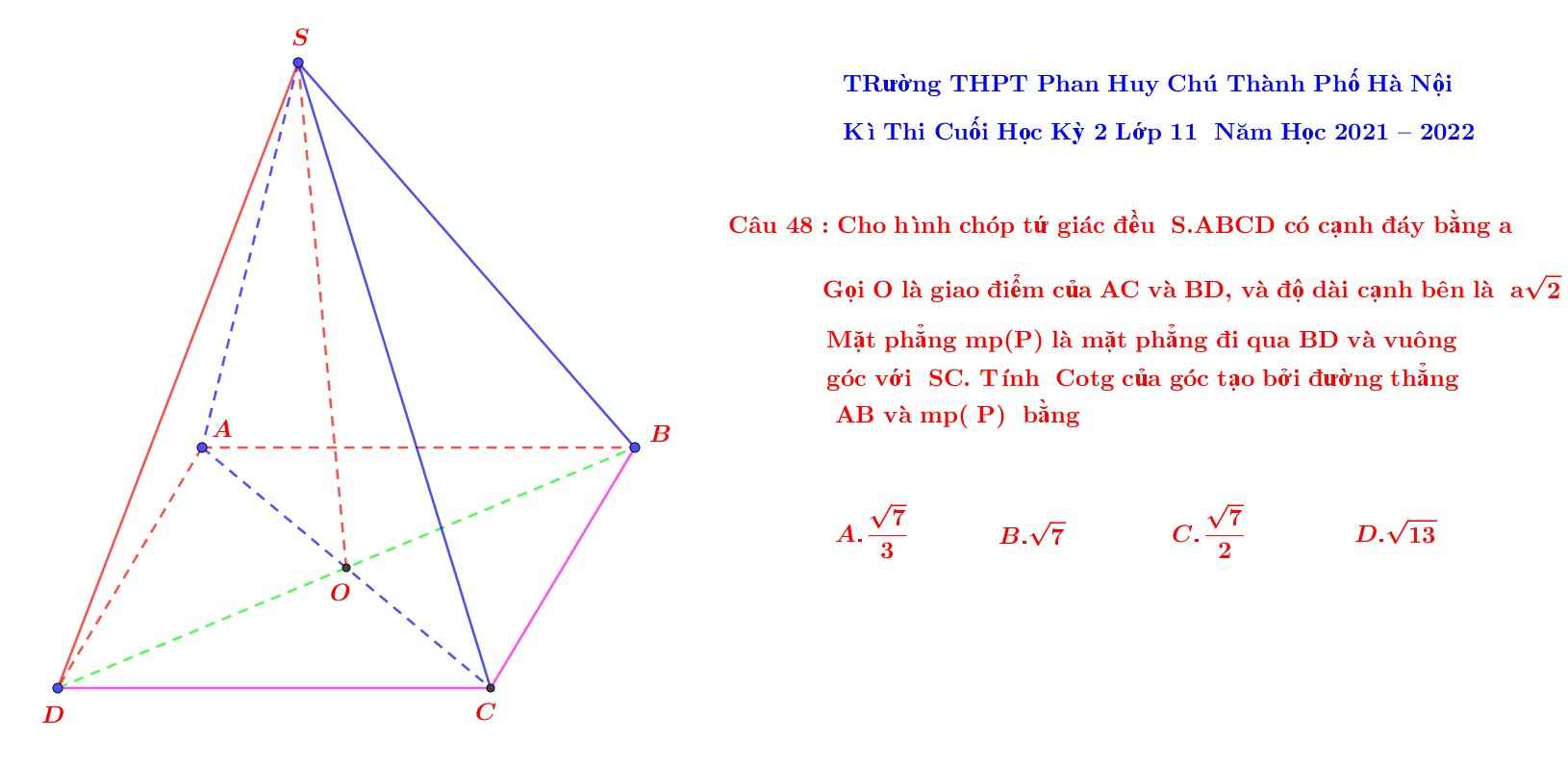
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA = 2a và vuông góc với mặt phẳng đáy. Gọi M là trung điểm cạnh SD. Tang của góc tạo bởi hai mặt phẳng (AMC) và (SBC) bằng
A. 3 2
B. 2 3 3
C. 5 5
D. 2 5 5
Chọn D
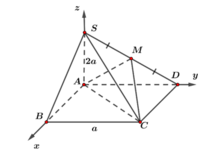
Để thuận tiện trong việc tính toán ta chọn a = 1.
Trong không gian, gắn hệ trục tọa độ Oxyz như hình vẽ sao cho gốc O trùng với điểm A, tia Ox chứa đoạn thẳng AB, tia Oy chứa đoạn thẳng AD, tia Oz chứa đoạn thẳng AS. Khi đó: A(0;0;0), B(1;0;0), C(1;1;0), S(0;0;2), D(0;1;0)
Vì M là trung điểm SD nên tọa độ là M 0 ; 1 2 ; 1
Ta có
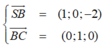
![]()
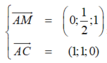
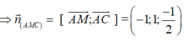
Gọi α là góc giữa hai mặt phẳng (AMC) và (SBC).
Suy ra
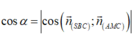
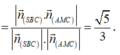
Mặt khác
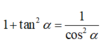
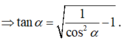
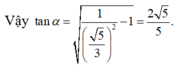
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA =2a và vuông góc với mặt phẳng đáy. Gọi M là trung điểm cạnh SD. Tang của góc tạo bởi hai mặt phẳng (AMC) và (SBC) bằng
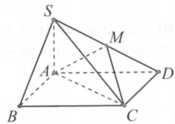
A. 5 5
B. 3 2
C. 2 5 5
D. 2 3 3
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB =a, AD = 2a Cạnh bên SA vuông góc với mặt phẳng đáy và cạnh bên SC tạo với đáy một góc 60 o Gọi M, N là trung điểm các cạnh bên SA và SB Khoảng cách từ điểm S đến mặt phẳng (DMN) bằng
A. 2 a 465 31
B. a 31 31
C. a 60 31
D. 2 a 5 31
Chọn A.

Xác định được
![]()
Vì M là trung điểm SA nên
![]()
Kẻ AK ⊥ DM và chứng minh được AK ⊥ (CDM) nên
![]()
Trong tam giác vuông MAD tính được
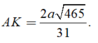
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với A B = a , A D = 2 a . Cạnh bên SA vuông góc với mặt phẳng đáy và cạnh bên SC tạo với đáy một góc 60 ° . Gọi M, N là trung điểm các cạnh bên SA và SB. Khoảng cách từ điểm S đến mặt phẳng (DMN) bằng
A. 2 a 465 31
B. a 31 60
C. a 60 31
D. 2 a 5 31
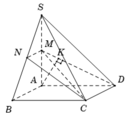
Xác định được ![]()
Vì M là trung điểm SA nên
![]()
Kẻ ![]() và chứng minh được
và chứng minh được ![]() nên
nên ![]()
Trong
∆
vuông MAD tính được ![]()
Chọn A.