Đồ thị hàm số y = 15 x 4 - 3 x 2 - 2018 cắt trục hoành tại bao nhiêu điểm ?
A. 4.
B. 2.
C. 1.
D. 3.
Cho hàm số y = (m -3)x + 3m + 7 (d) (m ≠3). Tìm m để:
1) Hàm số đồng biến?
2) Hàm số trên đi qua gốc tọa độ
3) Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng -2
4) Đồ thị hàm số cắt trục hoành tại điểm của hoành độ bằng 1
5) Đồ thị hàm số đi qua điểm A (-1; -2)
6) Đồ thị của hàm số đã cho với đồ thị của các hàm số y= -x + 5 và y = 2x-1 đồng quy
7) Tìm m để khoảng cách từ gốc tọa độ đến đường thẳng (d) lớn nhất
1: Để hàm số đồng biến thì m-3>0
hay m>3
2: Thay x=0 và y=0 vào (d), ta được:
3m+7=0
hay \(m=-\dfrac{7}{3}\)
Cho hàm số: (d): y=(3-m).x+m+1
a) Tìm m để hàm số là hàm số bậc nhất
b) Tìm m để đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng -2
c) Tìm m để đồ thị hàm số cắt đường thẳng y= -x+4 tại 1 điểm trên trục tung
d) Tìm m để đồ thị hàm số tạo với 2 trục tam giác có diện tích bằng 2
e) Tìm điểm cố định mà đồ thị hàm số luôn qua với mọi m
Cho hàm số y=f(x) xác định trên R. Đồ thị hàm số y = f ' ( x ) cắt trục hoành tại 3 điểm a, b, c ( a < b < c ) như hình dưới:
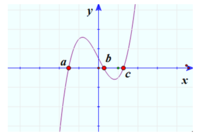
Biết f(b) < 0 Đồ thị hàm số y=f(x) cắt trục hoành tại bao nhiêu điểm phân biệt.
A. 4
B. 1
C. 0
D. 2
Đáp án D
Trên khoảng ( a ; b ) và ( c ; + ∞ ) hàm số đồng biến vì y'>0 đồ thị nằm hoàn toàn trên trục Ox
Hàm số nghịch biến trên các khoảng ( - ∞ ; a ) và (b;c) vì y'<0
Suy ra x=b là điểm cực đại mà y(b) <0 do đó trục hoành cắt đồ thị tại hai điểm phân biệt. Với d<0 ta có
Đồ thị hàm số y = 15 x 4 − 3 x 2 − 2018 cắt trục hoành tại bao nhiêu điểm?
A. 4 điểm
B. 2 điểm
C. 1 điểm
D. 3 điểm
Đáp án D
Giải pt 15 x 4 − 3 x 2 − 2018 = 0 ta được 2 nghiệm
Đồ thị hàm số y = 15 x 4 − 3 x 2 − 2018 cắt trục hoành tại bao nhiêu điểm?
A. 1 điểm.
B. 3 điểm.
C. 4 điểm.
D. 2 điểm.
Đáp án D
Phương pháp:
Xét sự tương giao của đồ thị hàm số y = f(x) với trục hoành.
Số giao điểm của đồ thị hàm số y = f(x) với trục hoành là số nghiệm của phương trình hoành độ giao điểm f(x) = 0
Cách làm:
Xét phương trình hoành độ giao điểm

Cho hàm số y = (m − 2)x + 5 có đồ thị là đường thẳng (d) (m là tham số, 𝑚 ≠ 2) a) Vẽ đồ thị hàm số trên với 𝑚 = 4 b) Tìm m để đồ thị hàm số cắt trục hoành tại điểm có hoành độ là 2. c) Tìm m để đồ thị cắt trục tung tại điểm có tung độ -3.
Cho hàm số y = (2+3m).x+4
a) Đồ thị cắt trục hoành tại điểm có hoành độ =2
b) tìm m để đồ thị hàm số cắt trục tung tại điểm có tung độ =4
a. Đồ thị cắt trục hoành tại điểm có hoành độ bằng 2
=> x = 2 và y = 0
=> 0 = (2 + 3m ) .2 + 4
<=> 2 + 3m = -2 <=> m = -4/3
b. Đồ thị cắt trục tung tại điểm có tug độ bằng 4 => x = 0 và y = 4
=> 4 = ( 2 + 3m) .0 + 4
<=> 4 = 4 luôn đúng với mọi m
Vậy mọi m thì đồ thị cắt trục tug tại điểm có tung độ bằng 4
Cho hàm số y = a x 3 + b x 2 + c x + d có đạo hàm là hàm số y=f'(x) có đồ thị như hình vẽ bên.
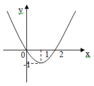
Biết rằng đồ thị hàm số y=f(x) tiếp xúc với trục hoành tại điểm có hoành độ dương. Hỏi đồ thị hàm số y=f(x) cắt trục tung tại điểm có tung độ bằng bao nhiêu?
A. 2 3
B. 1
C. 3 2
D. 4 3
Đáp án D
Ta có: y ' = 3 a x 2 + 2 b x + c
+) Đồ thị hàm số f'(x) đi qua gốc tọa độ => c=0
+) Đồ thị hàm số f'(x) có điểm cực trị:
1 ; − 1 ⇒ 6 a + 2 b = 0 3 a + 2 b = − 1 ⇔ a = 1 3 b = − 1
Vậy hàm số f ' x = x 2 − 2 x . Đồ thị hàm số f(x) tiếp xúc với trục hoành nên có cực trị nằm trên trục hoành. Các giá trị cực trị của hàm số f(x) là:
f 0 = d f 2 = 8 3 − 4 + d = − 4 3 + d
do điểm tiếp xúc có hoành độ dương
=> d = 4 3 => f(x) cắt trục tung tại điểm có tung độ 4 3
Cho hàm số y = ax 3 + bx 2 + cx + d có đạo hàm là hàm số y = f '(x) có đồ thị như hình vẽ bên. Biết rằng đồ thị hàm số y = f(x) tiếp xúc với trục hoành tại điểm có hoành độ dương. Hỏi đồ thị hàm số y = f(x)cắt trục tung tại điểm có tung độ bằng bao nhiêu?
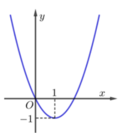
A. 2 3 .
B. 1
C. 3 2 .
D. 4 3 .