Cho hai số phức u, v thỏa mãn u = v = 10 và 3 u - 4 v = 2018 . Tính M = 4 u + 3 v
A. M = 2982
B. M = 50
C. M = 2018
D. M = 482
Cho hai số phức u, v thỏa mãn 3 u - 6 i + 3 u - 1 - 3 i = 5 10 , v - 1 + 2 i = v ¯ + i . Giá trị nhỏ nhất của u - v là:
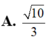
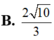
![]()
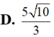
Biết có hai số u và v thỏa mãn u – v = 10 và u.v = 11. Tính |u+ v| ?
A. 11
B. 12
C. 10
D. 13
Đáp án B
Ta có: u.v =11 nên u.(-v) = -11 (1)
Từ u – v = 10 nên u + (- v) = 10 (2)
Khi đó; u và (-v) là nghiệm phương trình:
x 2 - 10 x - 11 = 0 (*)
Do a - b + c = 1 -(-10 ) + (-11) = 0 nên phương trình (*) có 2 nghiệm là:
x 1 = -1 và x 2 = 11
* Trường hợp 1: Nếu u = -1 và –v = 11
=> v = -11 nên u + v = -12
* Trường hợp 2: nếu u = 11 và –v = -1 thì v = 1
Suy ra: u + v = 12
Trong cả 2 trường hợp ta có: |u + v| = 12
Biết có hai số u và v thỏa mãn điều kiện: u + v = 12 và u.v = 27. Biết u < v. Tính u 2 .v?
A. 81
B. 27
C. 54
D. 243
Đáp án A
Hai số u, v cần tìm là nghiệm của phương trình:
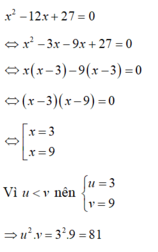
Cho các số phức z, w khác 0 và thỏa mãn |z-w| = 2|z| = |w|. Phẩn thực của số phức u = z w là:
A. a = 1 4
B. a = 1
C. a = 1 8
D. a = - 1 8
Cho các số phức z, w khác 0 và thỏa mãn |z-w| = 2|z| = |w| Phẩn thực của số phức u = z w là:
![]()
![]()
![]()
![]()
Cho số phức u và v. Xét các mệnh đề dưới đây
1. u + v = u + v
2. u − v = u − v
3. u . v = u . v
4. u v = u v v ≠ 0
Hỏi có bao nhiêu mệnh đề đúng trong 4 mệnh đề trên?
A. 1.
B. 2
C. 3
D. 4.
Đáp án B
Mệnh đề 1 và 2 sai; mệnh đề 3 và 4 đúng.
Cho số phức u và v. Xét các mệnh đề dưới đây
1. u + v = u + v
2. u − v = u − v
3. u . v = u . v
4. u v = u v v ≠ 0
Hỏi có bao nhiêu mệnh đề đúng trong 4 mệnh đề trên?
A. 1
B. 2
C. 3
D. 4
Đáp án B
Mệnh đề 1 và 2 sai; mệnh đề 3 và 4 đúng
Cho các vectơ u → , v → thỏa mãn u → = 5 2 , v → = 7 . Biểu thức ( u ⃗ + v ⃗ ) . ( u ⃗ - v ⃗ ) bằng
A. - 1
B. 1
C. 5 2 - 7
D. 7 - 5 2
Đáp án B
u → + v → . u → − v → = u → 2 − v → 2 = u → 2 − v → 2 = 5 2 2 − 7 2 = 1
Trong không gian với hệ tọa độ Oxyz cho vectơ u → = 2 ; - 1 ; 2 và vectơ đơn vị v → thỏa mãn u → - v → = 4 Độ dài của vectơ u → + v → bằng
A. 1
B. 2
C. 3
D. 4
Theo giả thiết, ta có 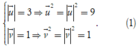
Từ
u
→
-
v
→
=
4
, suy ra ![]()
Kết hợp (1) và (2) ta được ![]()
Khi đó ![]()
Vậym | u → + v → | = 2
Chọn B.