Tìm tất cả các giá trị thực của tham số a (a >0) thỏa mãn 2 a + 1 2 1 2017 ≤ 2 2017 + 1 2 2017 a
A. 0< a≤ 2017.
B. 1< a< 2017.
C. a ≥2017.
D. 0< a< 1.
Tìm tất cả các giá trị thực của tham số a(a>0) thỏa mãn 2 a + 1 2 a 2017 ≤ 2 2017 + 1 2 2017 a
A. 0 < a < 1
B. 1 < a < 2017
C. a ≥ 2017
D. 0 < a ≤ 2017
Đáp án C
Ta có 2 a + 1 2 a 2017 ≤ 2 2017 + 1 2 2017 a ⇔ 1 + 4 a 2017 ≤ 1 + 4 2017 a ⇔ ln 1 + 4 a a ≤ ln 1 + 4 2017 2017
Xét hàm số f t = ln 1 + 4 t t với t ∈ 0 ; + ∞ ⇒ Hàm số nghịch biến trên khoảng 0 ; + ∞
Mà ln 1 + 4 a a ≤ ln 1 + 4 2017 2017 ⇔ f a ≤ f 2017 suy ra a ≥ 2017
Tìm tất cả các giá trị thực của tham số a sao cho hàm số ![]() đạt cực trị tại
đạt cực trị tại ![]() thỏa mãn:
thỏa mãn: ![]() .
.
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Tìm tất cả các giá trị của tham số m để phương trình 4 x - 3 . 2 x + 1 + m = 0 có hai nghiệm thực x 1 ; x 2 thỏa mãn x 1 + x 2 < 2 .
A. 0 < m < 2
B. m > 0
C. 0 < m < 4
D. m < 9
Cho hàm số y= 2x3-3( m+ 1) x2+ 6mx+ m3 với m là tham số thực. Tìm tất cả các giá trị của m để đồ thị hàm số có hai điểm cực trị A; B thỏa mãn AB = 2
A. m=0
B. m=0; m= 2.
C. m=1
D. m=2
Ta có
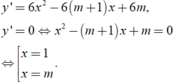
Để hàm số có hai điểm cực trị khi m khác -1
Tọa độ các điểm cực trị là A( 1; m3+ 3m-1) và B( m; 3m2)
Suy ra
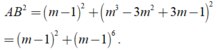
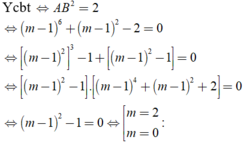
Chọn B.
S là tập hợp tất cả các giá trị thực của tham số a thỏa mãn mỗi nghiệm của bất phương trình log x ( 5 x 2 - 8 x + 3 ) > 2 đều là nghiệm của bất phương trình x 2 - 2 x - a 4 + 1 ≥ 0 . Khi đó:
A. S = - 10 5 ; 10 5 .
B. S = - ∞ ; - 10 5 ∪ 10 5 ; + ∞
C. S = - 10 5 ; 10 5 .
D. S = - ∞ ; - 10 5 ∪ 10 5 ; + ∞ .
Tìm tất cả các giá trị thực của tham số m để hàm số y = m 3 x 3 + 2 x 2 + m x + 1 có 2 điểm cực trị thỏa mãn x C Đ < x C T .
A. m < 2
B. -2 < m < 0
C. -2 < m <2
D. 0 < m < 2.
Tìm tất cả các giá trị thực của tham số m để hàm số y = m 3 x 3 + 2 x 2 + m x + 1 có 2 điểm cực trị thỏa mãn x C D < x C T
A. m < 2
B. − 2 < m < 0
C. − 2 < m < 2
D. 0 < m < 2
Đáp án D
Ta có y = m 3 x 3 + 2 x 2 + m x + 1 ⇒ y ' = m x 2 + 4 x + m ; ∀ x ∈ ℝ
Phương trình y ' = 0 ⇔ m x 2 + 4 x + m = 0 , có Δ = 4 − m 2
Yêu cầu bài toán tương đương với a = m 3 > 0 Δ ' > 0 ⇔ m > 0 4 − m 2 > 0 ⇔ 0 < m < 2
Tìm tất cả các giá trị thực của tham số m để hàm số y = m 3 x 3 + 2 x 2 + m x + 1 có 2 điểm cực trị thỏa mãn x C D < x C T
A. 0 < m < 2
B. -2 < m < 0
C. m < 2
D. -2 < m 2
Tìm tất cả các giá trị thực của tham số m để hàm số y = m 3 x 3 + 2 x 2 + m x + 1 có 2 điểm cực trị thỏa mãn điều kiện x C D < x C T .
A. m < 2
B. -2 < m < 0
C. -2 < m < 2
D. 0 < m < 2