Cho đoạn thẳng AB, điểm M di chuyển trên đoạn thẳng ấy. Vẽ về một phía của AB các tam giác đều AMD, BME. Trung điểm I của DE di chuyển trên đường nào?

Những câu hỏi liên quan
Cho đoạn thẳng AB, điểm M di chuyển trên đoạn thẳng ấy. Vẽ về một phía của AB các tam giác đều AMD, BME. Trung điểm I của DE di chuyển trên đường nào ?
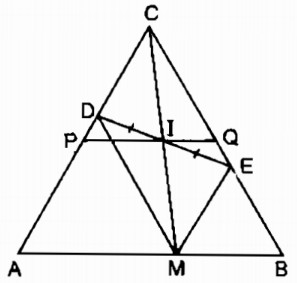
Gọi giao điểm của AD và BE là C.
∆ ABC có: ˆA=600A^=600 (vì ∆ ADM đều)
ˆB=600B^=600 (vì ∆ BEM đều)
Suy ra: ∆ ABC đều, AC = AB = BC nên điểm C cố định
ˆA=ˆEMB=600A^=EMB^=600
⇒ ME // AC (vì có cặp góc đồng vị bằng nhau)
hay ME // DC
ˆDMA=ˆB=600DMA^=B^=600
⇒ MD // BC (vì có cặp góc đồng vị bằng nhau)
hay MD // EC
Tứ giác CDME là hình bình hành
I là trung điểm của DE nên I là trung điểm của CM
Kẻ CH ⊥ AB, IK ⊥ AB ⇒ IK // CH
Trong ∆ CHM ta có:
CI = IM
IK // CH
nên IK là đường trung bình của ∆ CHM ⇒ IK = 1212CH
C cố định ⇒ CH không đổi ⇒ IK =1212CH không thay đổi nên I chuyển động trên đường thẳng song song AB, cách AB một khoảng bằng 1212CH.
Khi M trùng với A thì I trùng trung điểm P của AC.
Khi M trùng với B thì I trùng với trung điểm Q của BC.
Vậy khi M chuyển động trên đoạn thẳng AB thì I chuyển động trên đoạn PQ (P là trung điểm của AC, Q là trung điểm của BC)
Xem thêm tại: http://sachbaitap.com/cau-129-trang-96-sach-bai-tap-sbt-toan-8-tap-1-c6a8515.html#ixzz4zLYSfxii
Đúng 0
Bình luận (0)
CHO ĐOẠN THẲNG AB .M LÀ 1 ĐIỂM DI ĐỘNG TRÊN AB . VẼ VỀ 1 PHÍA CỦA ĐOẠN AB CÁC TAM GIÁC ĐỀU AMD, BME. HỎI TRUNG ĐIỂM I CỦA ĐOẠN DE CHUYỂN ĐỘNG TRÊN ĐƯỜNG NÀO?
Cho đoạn thẳng AB, điểm M di chuyển trên đoạn thẳng ấy. Vẽ về một phía của AB các tam giác đều AMD, BME. Trung điểm I của DE di chuyển trên đường nào?
(Ai có cách trình bày đúng thì làm hộ mình nhé. Viết lời giải đầy đủ và vẽ hình nếu vẽ được. Ai đúng mình tick cho. thanks ;D)
Cho đường thẳng AB . điểm M là một điểm thuộc AB . Vẽ về một phía của AB các tam giác đều AMD và BME . Gọi I là trung điểm của DE . Khi M di chuyển trên AB thì I di chuyển trên đương nào ?
bài 8 Cho đoạn thẳng AB và M là điểm bất kì thuộc đoạn thẳng đó. Vẽ về một phía của AB các tam giác đều AMD , BME . Gọi I là trung điểm của đoạn thẳng DE. Khi M di chuyển trên đường thẳng AB:
a, chứng minh MI luôn đi qua giao điểm của AD , BE.
B, điểm I di chuyển trên đường nào ?
bài 8 Cho đoạn thẳng AB và M là điểm bất kì thuộc đoạn thẳng đó. Vẽ về một phía của AB các tam giác đều AMD , BME . Gọi I là trung điểm của đoạn thẳng DE. Khi M di chuyển trên đường thẳng AB:
a, chứng minh MI luôn đi qua giao điểm của AD , BE.
B, điểm I di chuyển trên đường nào ?
bài 1: Cho đoạn thẳng AB và M là điểm bất kì thuộc đoạn thẳng đó. Vẽ về một phía của AB các tam giác đều AMD , BME . Gọi I là trung điểm của đoạn thẳng DE. Khi M di chuyển trên đường thẳng AB:a, chứng minh MI luôn đi qua giao điểm của AD , BE.B, điểm I di chuyển trên đường nào ?Bài 2: Cho đoạn thẳng AB bằng 6 cm và M là điểm bất kì thuộc đoạn thẳng AB . vẽ tia Mx vuông góc với AB . lấy N,P thuộc tia Mx sao cho MN AM và MPMB . Gọi I,K lần lượt là trung điểm của các đoạn thẳng AN , PB và O là...
Đọc tiếp
bài 1: Cho đoạn thẳng AB và M là điểm bất kì thuộc đoạn thẳng đó. Vẽ về một phía của AB các tam giác đều AMD , BME . Gọi I là trung điểm của đoạn thẳng DE. Khi M di chuyển trên đường thẳng AB:
a, chứng minh MI luôn đi qua giao điểm của AD , BE.
B, điểm I di chuyển trên đường nào ?
Bài 2: Cho đoạn thẳng AB bằng 6 cm và M là điểm bất kì thuộc đoạn thẳng AB . vẽ tia Mx vuông góc với AB . lấy N,P thuộc tia Mx sao cho MN = AM và MP=MB . Gọi I,K lần lượt là trung điểm của các đoạn thẳng AN , PB và O là trung điểm của đoạn thẳng IK
a, tính độ dài khoảng cách từ O tới AB
b, Gọi C là giao điểm của tia AI và tia BP. Chứng minh rằng khi M di chuyển trên đoạn thẳng AB thì C luôn cố định
c, khi điểm M di chuyển trên đoạn thẳng AB thì điểm O di chuyển trên đường nào ?
·
Cho đoạn thẳng AB, điểm M chuyển động trên đoạn thẳng AB. Vẽ về cùng về một phía của nửa mặt phẳng bờ AB các tam giác đều AMC và BMD. Trung điểm I của đoạn CD di chuyển trên đường nào?
Tương tự 2B. Gợi ý: Kéo dài AC và BD cắt nhau tại E. Xét các trường hợp khi M º A Þ C º A, D º E và khi M º B Þ D º B, C º E.
Từ đó chứng minh được I thuộc đường trung bình của DABE.
Đúng 0
Bình luận (0)
Cho đoạn thẳng AB, điểm M chuyển động trên đoạn thẳng AB. Vẽ về một phía của nửa mặt phẳng bờ AB các tam giác AMC vuông cân tại C và tam giác BMD vuông cân tại D. Trung điểm I của đoạn CD di chuyển trên đường nào?
Tương tự bài 4. kéo dài AC và BD cắt nhau tại E. Từ đó chứng minh được I thuộc đường trung bình của DABE.
Đúng 0
Bình luận (1)









