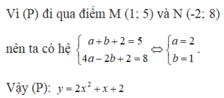Xác định parabol y = ax2 + bx + 2, biết rằng parabol đó: Đi qua hai điểm M(1; 5) và N(-2; 8)

Những câu hỏi liên quan
Xác định parabol y = ax2 + bx + 2, biết rằng parabol đó: Đi qua hai điểm A(3; -4) và có trục đối xứng là x = -3/2
+ Parabol y = ax2 + bx + 2 có trục đối xứng x = –3/2
⇒ –b/2a = –3/2 ⇒ b = 3a (1)
+ Parabol y = ax2 + bx + 2 đi qua điểm A(3; –4)
⇒ –4 = a.32 + b.3 + 2 ⇒ 9a + 3b = –6 (2).
Thay b = 3a ở (1) vào biểu thức (2) ta được:
9a + 3.3a = –6 ⇒ 18a = –6 ⇒ a = –1/3 ⇒ b = –1.
Vậy parabol cần tìm là y = –1/3x2 – x + 2.
Đúng 0
Bình luận (0)
Xác định parabol y = ax2 + bx + 2, biết rằng parabol đó: Đi qua điểm B(-1; 6) và tung độ của đỉnh là -1/4.
+ Parabol y = ax2 + bx + 2 đi qua điểm B(–1 ; 6)
⇒ 6 = a.( –1)2 + b.( –1) + 2 ⇒ a = b + 4 (1)
+ Parabol y = ax2 + bx + 2 có tung độ của đỉnh là –1/4
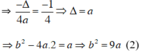
Thay (1) vào (2) ta được: b2 = 9.(b + 4) ⇔ b2 – 9b – 36 = 0.
Phương trình có hai nghiệm b = 12 hoặc b = –3.
Với b = 12 thì a = 16.
Với b = –3 thì a = 1.
Vậy có hai parabol thỏa mãn là y = 16x2 + 12b + 2 và y = x2 – 3x + 2.
Đúng 1
Bình luận (0)
Xác định parabol (P): y = ax2 + bx + c biết rằng parabol (P) đi qua ba điểm A(1; 1), B(-1; -3) và O(0; 0).
A. y = x2 + 2x.
B. y = -x2 – 2x.
C. y = -x2 + 2x.
D. y = x2 – 2x.
Vì parabol đi qua ba điểm A, B, C nên ta có hệ phương trình:
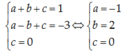
Vậy (P): y = -x2 + 2x
Chọn C.
Đúng 0
Bình luận (0)
Xác định Parabol (P):
y
ax
2
+
b
x
−
5
biết rằng Parabol đi qua điểm A (3; -4)và có trục đối xứng x
-
3
2
A.
y
1
18
x
2
+
1
6
x
−
5
B.
y
1...
Đọc tiếp
Xác định Parabol (P): y = ax 2 + b x − 5 biết rằng Parabol đi qua điểm A (3; -4)và có trục đối xứng x = - 3 2
A. y = 1 18 x 2 + 1 6 x − 5
B. y = 1 18 x 2 + 1 6 x + 5
C. y = 3 x 2 + 9 x − 9
D. y = − 1 18 x 2 + 1 6 x − 5
Xác định Parabol (P): y a
x
2
+ bx + 2 biết rằng Parabol đi qua hai điểm M (1; 5) và N (2; −2). A. y −5
x
2
+ 8x + 2 B. y 10
x
2
+ 13x + 2 C. y −10
x
2
− 13x + 2 D. y 9
x
2
+ 6x – 5
Đọc tiếp
Xác định Parabol (P): y = a x 2 + bx + 2 biết rằng Parabol đi qua hai điểm M (1; 5) và N (2; −2).
A. y = −5 x 2 + 8x + 2
B. y = 10 x 2 + 13x + 2
C. y = −10 x 2 − 13x + 2
D. y = 9 x 2 + 6x – 5
Xác định parabol y = ax2 + bx + 2, biết rằng parabol đó: Có đỉnh là I(2; -2)
Parabol y = ax2 + bx + 2 có đỉnh I(2 ; –2), suy ra :
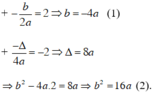
Từ (1) ⇒ b2 = 16.a2, thay vào (2) ta được 16a2 = 16a ⇒ a = 1 ⇒ b = –4.
Vậy parabol cần tìm là y = x2 – 4x + 2.
Đúng 0
Bình luận (0)
Xác định parabol (P): y = ax2 + bx + c biết rằng (P) đi qua M(-5; 6) và cắt trục tung tại điểm có tung độ bằng -2. Mệnh đề nào dưới đây đúng?
A. a = 6b.
B. 25a – 5b = 8.
C. b = -6a.
D. 25a + 5b = 8.
Parabol đi qua điểm M suy ra 6 = 25a – 5b + c (1)
Parabol cắt Oy tại điểm có tung độ bằng -2 nên -2 = a.0 + b.0 + c hay c = -2
Vậy 25a – 5b = 8
Chọn B.
Đúng 0
Bình luận (0)
xác định hàm số bậc hai ax2+bx+c biết rằng đồ thị hàm số là parabol đi qua điểm B<0,4> và có đỉnh I <1,5>
Theo đề, ta có: c=4
Theo đề, ta có:
\(\left\{{}\begin{matrix}-\dfrac{b}{2a}=1\\-\dfrac{b^2}{16a}=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=-2a\\4a^2+80a=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-20\\b=40\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Xác định parabol (P): y a
x
2
+ bx + 2, biết rằng (P) đi qua hai điểm M (1; 5) và N (−2; 8). A. y 2
x
2
+ x + 2. B. y
x
2
+ x + 2. C. y −2
x
2
+ x + 2. D. y −2
x
2
– x + 2.
Đọc tiếp
Xác định parabol (P): y = a x 2 + bx + 2, biết rằng (P) đi qua hai điểm M (1; 5) và N (−2; 8).
A. y = 2 x 2 + x + 2.
B. y = x 2 + x + 2.
C. y = −2 x 2 + x + 2.
D. y = −2 x 2 – x + 2.