Cho góc bẹt AOB. Trên cùng một nửa mặt phẳng bờ AB vẽ các tia OM và ON sao cho A O M ^ = B O N ^ = m ° ( 90 < m < 180 ) . Vẽ tia phân giác OC của góc MON.
a) Chứng tỏ rằng O C ⊥ A B .
b) Xác định giá trị của m để O M ⊥ O N .
Cho góc bẹt AOB. Trên cùng một nửa mặt phẳng bờ AB, vẽ các tia OM, OC sao cho AOM và BOC lần lươt bằng 50 và 80 độ.Chứng tỏ rằng OM la tia phân giác của góc AOB.
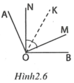
Cho góc bẹt AOB. Trên cùng một nửa mặt phẳng bờ AB vẽ các tia OE, OF sao cho A O E ^ = B O F ^ < 90 ° . Vẽ tia phân giác OM của góc EOF. Chứng tỏ rằng O M ⊥ A B
* Tìm cách giải
Để chứng tỏ O M ⊥ A B ta cần chứng tỏ góc AOM (hoặc góc BOM) có số đo bằng 90 ° .
* Trình bày lời giải
Ta có A O E ^ = B O F ^ ; M O E ^ = M O F ^ (đề bài cho)
⇒ A O E ^ + M O E ^ = B O F ^ + M O F ^ (1)
Tia OE nằm giữa hai tia OA, OM; tia OF nằm giữa hai tia OB, OM nên từ (1) suy ra A O M ^ = B O M ^ . Mặt khác, A O M ^ + B O M ^ = 180 ° (hai góc kề bù) nên A O M ^ = 180 ° : 2 = 90 ° , suy ra O M ⊥ O A . Do đó O M ⊥ A B
cho góc bẹt AOB . Trên cùng một nửa mặt phẳng bờ là AB vẽ hai tia OM và ON sao cho góc AOM =BON < 90o
và tia OC là tia phân giác của góc MON . Chứng tỏ rằng OC vuông góc với AB
\(\Rightarrow\widehat{AOM}=\widehat{BON}\)
\(\Rightarrow\widehat{AOM}+\widehat{MOC}+\widehat{CON}+\widehat{NOB}=180^o\)
Mà: \(\widehat{AOM}=\widehat{BON},\widehat{CON}=\widehat{COM}\)
\(\Rightarrow2\widehat{AOM}+2\widehat{MOC}=180^o\)
\(\Rightarrow\widehat{AOM}+\widehat{MOC}=90^o\Leftrightarrow\widehat{AOC}=90^o\)
\(\Rightarrow CO\perp AB\)
cho góc bẹt AOB . Trên cùng một nửa mặt phẳng bờ là AB vẽ hai tia OM và ON sao cho góc AOM =BON < 90o
và tia OC là tia phân giác của góc MON . Chứng tỏ rằng OC vuông góc với AB
Vì góc AOB là góc bẹt => góc AOB = 180 độ
Vì góc AOM = BON mà OC là tia phân giác của góc MON => MOC = NOC =1/2 MON
=> AOM+MOC=BON+NOC
=> AOC = BOC mà AOC+BOC= AOB
=> AOC = BOC = 180 : 2= 90 độ
=> AOC VÀ BOC là góc vuông và OC cắt AB tại O=> OC vuông góc AB
Cho góc bẹt AOB. Trên cùng một nửa mặt phẳng bờ là AB ta vẽ hai tia OM,ON sao cho AOM=MON=140 độ và vẽ tia OC là tia phân giác của góc MON. Chứng minh rằng OC vuông góc với AB.
Cho góc bẹt AOB. Trên cùng nửa mặt phẳng bờ AB vẽ 3 tia OM,ON và OC sao cho AOM=BON<\(90^o\)và tia OC là Tia pg của MON. CMR OC vuông góc với AB
Cho góc bẹt AOB. Trên cùng một nửa mặt phẳng bờ AB , vẽ tia OE và OF sao cho AOE=BÒ=55 độ . Vẽ tia OM ơn trong góc EOF sao cho OM vuông góc với AB. Chứng minh rằng: tia OM là tia phân giác của EOF?
Ta có:
- Góc AOE = BOE = 55 độ (do AOE = BO = 55 độ)
- Góc EOF = 180 - (AOE + BO) = 180 - (55 + 55) = 70 độ
Vì OM vuông góc với AB, nên góc MOE = góc MOF (do cùng là góc vuông).
Vậy, ta đã chứng minh được rằng tia OM là tia phân giác của góc EOF.
--thodagbun--
Cho góc bẹt AOB . trên cùng một nửa mặt phẳng bờ chứa AB vẽ ba tia OM,ON và OC sao cho AOM = BON < 90 độ và tia OC là tia phân giác của MON. chứng tỏ rằng OC vuộng góc với AB
tia Om nằm giữa hai tia OA và OC ; tia ON nằm giữa hai tia OB và OC
do đó : \(\widehat{COA}=\widehat{O_3}+\widehat{O_1}\)và \(\widehat{COB}=\widehat{O_4}+\widehat{O_2}\)
vì \(\widehat{O_1}=\widehat{O_2}\)( gt ) ; \(\widehat{O_3}=\widehat{O_4}\)( vì tia OC là tia phân giác của \(\widehat{MON}\)) nên \(\widehat{COA}=\widehat{COB}\)
\(\widehat{COA}\)và \(\widehat{COB}\)là hai góc kề bù bằng nhau nên \(\widehat{COA}=180^o:2=90^o\)suy ra \(OC⊥AB\)
cho góc bẹt AOB, trên cùng 1 nửa mặt phẳng bờ AB vẽ 2 tia OM và ON sao cho AOM=BON = 40 độ.Vẽ tia OC là tia đối của tia OM . Chứng minh OB là tia phân giác của góc NOC
OM và OC là 2 tia đối nhau=>MOC=180o
=>MOA+AOC=MOC
=>AOC=MOC-MOA
=180o-40o
=140o
vì AOB=180o=>AOC+COB=AOB
=>COB=AOB-AOC=180o-140o=40o
vì OM và ON nằm cùng 1 nửa mặt phẳng mà OC đối nhau với OM
=>OC và ON nằm trên 2 nửa mặt phẳng khác nhau
=>NOB và BOC kề nhau
=>OB nằm giữa ON và OC
=>NOB+BOC=NOC
mà NOB=BOC=40o
=>OB là tia phân giác của NOC
=>đpcm