Cho tam giác ABC nội tiếp trong đường tròn tâm O, biết góc A = 32 ° , góc B = 84 ° . Lấy các điểm D, E, F thuộc đường tròn (O) sao cho AD = AB, BE = BC, CF = CA . Hãy tính các góc của tam giác DEF

Những câu hỏi liên quan
Cho tam giác ABC nội tiếp đường tròn tâm O, biết \(\widehat{A}=32^0,\widehat{B}=84^0\). Lấy các điểm D, E, F thuộc đường tròn () sao cho AD = AB, BE = BC, CF = CA.
Hãy tính các góc của tam giác DEF ?
Cho tam giác ABC nhọn nội tiếp trong đường tròn tâm O. Các đường cao BD và CE của tam giác cắt nhau tại H. Chứng minh rằng rằng:
A) Tứ giác BCDE nội tiếp đường tròn, từ đó suy ra góc BCD = góc AED
B) Kẻ đường kính AK, chứng minh AB.BC = AK.BD
C) Từ điểm O kẻ OM vuông góc với BC Chứng minh H, K, M thẳng hàng
cho tam giác ABC nội tiếp (O) biết góc A =32, góc B= 84 Lấy D,E,F thuộc (O) sao cho AD=AB, BE=BC,CF=CA. Tính các góc của tam giác DEF
cho tam giác nhọn ABC nội tiếp đường tròn tâm O. M là điểm chính giữa cung BC không chứa điểm A. Gọi M là điểm đối xứng với M qua O. Các đường phân giác trong góc B và góc C của tam giác ABC cắt đường thẳng AM lần lượt tại E và F.1/Chứng minh tứ giác BCEF nội tiếp được trong đường tròn2/Biết đường tròn nội tiếp tam giác ABC có tâm I bán Kính r.Chứng Minh: IB.IC 2r.IM
Đọc tiếp
cho tam giác nhọn ABC nội tiếp đường tròn tâm O. M là điểm chính giữa cung BC không chứa điểm A. Gọi M' là điểm đối xứng với M qua O. Các đường phân giác trong góc B và góc C của tam giác ABC cắt đường thẳng AM' lần lượt tại E và F.
1/Chứng minh tứ giác BCEF nội tiếp được trong đường tròn
2/Biết đường tròn nội tiếp tam giác ABC có tâm I bán Kính r.
Chứng Minh: IB.IC = 2r.IM
Cho đường tròn tâm O, bán kính R = 10cm. Tam giác ABC nội tiếp đường tròn tâm O, biết góc A là góc tù. Hỏi trong các dây AB, BC và AC thì dây nào gần tâm nhất?
A. AB
B. AC
C. BC
D. Chưa kết luận được
Đáp án C
Tam giác ABC có góc A là góc tù nên 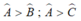
Mà cạnh đối diện với góc A là cạnh BC .
Áp dụng định lí: trong 1 tam giác cạnh đối diện với góc lớn hơn thì lớn hơn ta được:
BC > AC và BC > AB
Vậy tam giác ABC có độ dài cạnh BC là lớn nhất nên dây BC gần tâm nhất.
Chưa thể kết luận dây nào xa tâm nhất.
Đúng 0
Bình luận (0)
cho tam giác ABC có ba góc nhọn . các đường cao AD,BE,CF của tam giác ABC cắt nhau tại H
a) Chứng minh CEHD nội tiếp trong một đường tròn . xác định vị trí tâm O của đường tròn ngoại tiếp tứ giác CEHD
b) chứng minh góc FEH= góc DEH
Chứng minh H là tâm đường tròn nội tiếp tam giác DEF
c)cho CH= 4cm. Tính độ dài đường tròn (O) và diện tích hình tròn (O)
Cho tam giác ABC có ba góc đều nhọn nội tiếp đường tròn tâm O, các đường cao BM,CN của tam giác cắt nhau tại H. Cho cạnh BC cô định, A thay đổi trên cung lớn BC sao cho tam giác ABC luôn nhọn. Xác định vị trí điể A để diện tích tam giác BCH lớn nhất
Tam giác ABC nội tiếp đường tròn tâm O. Biết gốc B= 32°; gốc C= 40°. Tính số đo góc ở tâm BOC
Có góc A= 180*-32*-40*=108*
Có góc BOC là góc ở tâm
=> Góc BOC= 108*/2=54*
Cho tam giác ABC có các góc là góc nhọn và nội tiếp đường tròn tâm (O). Tiếp tuyến của đường tròn tâm (O) tại B,C cắt nhau tại D
a) Chứng minh OCDB nội tiếp
b) Gọi H là trực tâm của tam giác ABC. M là trung điểm của BC
Chứng minh AH=2OM
a) Xét tứ giác OCDB có
\(\widehat{OBD}+\widehat{OBC}=180^0\)
Do đó: OCDB là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Đúng 0
Bình luận (0)


















