Các câu hỏi tương tự
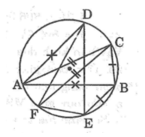
cho tam giác ABC nội tiếp (O) biết góc A =32, góc B= 84 Lấy D,E,F thuộc (O) sao cho AD=AB, BE=BC,CF=CA. Tính các góc của tam giác DEF
Cho tam giác ABC có 3 góc nhọn, nội tiếp đường tròn tâm O và AB<AC. Vẽ đường kính AD của đường tròn (O). Kẻ BE và CF vuông góc với AD( E,F thuộc AD). Kẻ AH vuông góc với AC(H thuộc BC).
a) Chứng minh 4 điểm A,B,H,E cùng nằm trên một đường tròn và tam giác ABH đồng dạng với tam giác ADC.
b) Chứng minh HE // CD
c) Gọi M là trung điểm của BC. Chuwngd minh ME=MF.
cho tam giác ABC có ba góc nhọn . các đường cao AD,BE,CF của tam giác ABC cắt nhau tại H
a) Chứng minh CEHD nội tiếp trong một đường tròn . xác định vị trí tâm O của đường tròn ngoại tiếp tứ giác CEHD
b) chứng minh góc FEH= góc DEH
Chứng minh H là tâm đường tròn nội tiếp tam giác DEF
c)cho CH= 4cm. Tính độ dài đường tròn (O) và diện tích hình tròn (O)
Cho tam giác ABC không cân nội tiếp đường tròn (O) , AD là đường cao của tam giác ABC . Vẽ BE vuông góc với OA tại E , CF vuông góc với OA tại F . Chứng minh rằng M là tâm đường tròn ngoại tiếp tam giác DEF.
cho tam giác ABC có ba góc nhọn nội tiếp đường tròn tâm O bán kính R . Kẻ đường cao AD (D thuộc BC) và đường kính AK . Hạ BE và CF cùng vuông góc với AK ( E thuộc AK , F thuộc AK ).1) chứng minh tứ giác ABDE nội tiếp.2) Chứng minh DF song song với BK3) cho góc ABC 60 độ , R4cm. Tính diện tích hình quạt giới hạn bởi OC , OK và cung nhỏ CK .4) cho BC cố định , A chuyển động trên cung lớn Bc sao cho tam giác ABC có ba góc nhọn . Chứng minh tâm đường tròn ngoại tiếp tam giác DEF là một điểm cố địn...
Đọc tiếp
cho tam giác ABC có ba góc nhọn nội tiếp đường tròn tâm O bán kính R . Kẻ đường cao AD (D thuộc BC) và đường kính AK . Hạ BE và CF cùng vuông góc với AK ( E thuộc AK , F thuộc AK ).
1) chứng minh tứ giác ABDE nội tiếp.
2) Chứng minh DF song song với BK
3) cho góc ABC = 60 độ , R=4cm. Tính diện tích hình quạt giới hạn bởi OC , OK và cung nhỏ CK .
4) cho BC cố định , A chuyển động trên cung lớn Bc sao cho tam giác ABC có ba góc nhọn . Chứng minh tâm đường tròn ngoại tiếp tam giác DEF là một điểm cố định.
Cho tam giác ABC nhọn (ABAC) nội tiếp đường tròn (O), các đường cao AD, BE, CF của tam giác ABC đồng quy tại K.a) chứng minh các tứ giác AEKF và BCEF nội tiếp, định vị tâm của mỗi đường tròn ngoại tiếp tứ giác đó.b) chứng minh EK là tia phân giác góc DEF và cho biết vị trí đặc biệt của K đối với tam giác DEF.c) BC cắt EF tại S, SA cắt đường tròn (O) tại điểm thứ 2 là T. chứng minh tứ giác ATEF nội tiếp và tính góc ATK.d) chứng minh AE.FTAF.ET+AT.FE
Đọc tiếp
Cho tam giác ABC nhọn (AB<AC) nội tiếp đường tròn (O), các đường cao AD, BE, CF của tam giác ABC đồng quy tại K.
a) chứng minh các tứ giác AEKF và BCEF nội tiếp, định vị tâm của mỗi đường tròn ngoại tiếp tứ giác đó.
b) chứng minh EK là tia phân giác góc DEF và cho biết vị trí đặc biệt của K đối với tam giác DEF.
c) BC cắt EF tại S, SA cắt đường tròn (O) tại điểm thứ 2 là T. chứng minh tứ giác ATEF nội tiếp và tính góc ATK.
d) chứng minh AE.FT=AF.ET+AT.FE
Cho tam giác ABC nhọn nội tiếp đường tròn (O).H là trực tâm của tam giác ABC,AD là đường kính của (O).,E thuộc AC sao cho HE song song với BC.a,CMR các đường thẳng BH,DE cắt nhau tại 1 điểm thuộc đường tròn (O). b,Gọi F là giao điểm của EH và AB.CMR A thuộc đường tròn bàng tiếp ứng với đỉnh D của tam giác DEF. c,Gọi I là tâm đường tròn nội tiếp tam giác DEF.CMR các đường thẳng BE,CF,IH đồng quyGiúp mình câu c với
Đọc tiếp
Cho tam giác ABC nhọn nội tiếp đường tròn (O).H là trực tâm của tam giác ABC,AD là đường kính của (O).,E thuộc AC sao cho HE song song với BC.
a,CMR các đường thẳng BH,DE cắt nhau tại 1 điểm thuộc đường tròn (O).
b,Gọi F là giao điểm của EH và AB.CMR A thuộc đường tròn bàng tiếp ứng với đỉnh D của tam giác DEF.
c,Gọi I là tâm đường tròn nội tiếp tam giác DEF.CMR các đường thẳng BE,CF,IH đồng quy
Giúp mình câu c với
Cho đường tròn (O) có dây BC cố định không đi qua tâm O. Điểm A chuyển động trên đường tròn (O) sao cho tam giác ABC có 3 góc nhọn. Kẻ các đường cao BE và CF của tam giác ABC (E thuộc AC, F thuộc AB). Chứng minh rằng : a) BCEF là tứ giác nội tiếp. b) EF.AB = AE.BC. c) Độ dài đoạn thẳng EF không đổi khi A chuyển động.
Bài 1. Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O). Các đường cao AD, BE, CF cắt nhau tại H và cắt đường tròn (O) lần lượt tại M,N,P.Chứng minh rằng: Tứ giác CEHD, nội tiếp .Bốn điểm B,C,E,F cùng nằm trên một đường tròn.AE.AC AH.AD; AD.BC BE.AC.H và M đối xứng nhau qua BC.Xác định tâm đường tròn nội tiếp tam giác DEF.Bài 2. Cho tam giác cân ABC (AB AC), các đường cao AD, BE, cắt nhau tại H. Gọi O là tâm đường tròn ngoại tiếp tam giác AHE.Chứng minh tứ giác CEHD nội tiếp .Bốn điểm...
Đọc tiếp
Bài 1. Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O). Các đường cao AD, BE, CF cắt nhau tại H và cắt đường tròn (O) lần lượt tại M,N,P.
Chứng minh rằng: Tứ giác CEHD, nội tiếp .Bốn điểm B,C,E,F cùng nằm trên một đường tròn.AE.AC = AH.AD; AD.BC = BE.AC.H và M đối xứng nhau qua BC.Xác định tâm đường tròn nội tiếp tam giác DEF.Bài 2. Cho tam giác cân ABC (AB = AC), các đường cao AD, BE, cắt nhau tại H. Gọi O là tâm đường tròn ngoại tiếp tam giác AHE.
Chứng minh tứ giác CEHD nội tiếp .Bốn điểm A, E, D, B cùng nằm trên một đường tròn.Chứng minh ED = 1/2BC.Chứng minh DE là tiếp tuyến của đường tròn (O).Tính độ dài DE biết DH = 2 Cm, AH = 6 Cm.