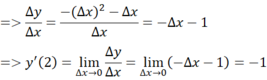Cho hàm số y = cos3x.sin2x. Tính 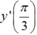 bằng:
bằng:
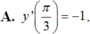
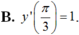
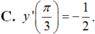
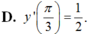
Cho hàm số y = cos 3 x . sin 2 x . Tính y ' π 3 bằng
A. y ' π 3 = − 1
B. y ' π 3 = 1
C. y ' π 3 = − 1 2
D. y ' π 3 = 1 2
Chọn B
y ' = cos 3 x ' sin 2 x + cos 3 x sin 2 x ' = − 3 sin 3 x . sin 2 x + 2 cos 3 x . cos 2 x
y ' π 3 = − 3 sin 3 π 3 . sin 2 π 3 + 2 cos 3 π 3 . cos 2 π 3 = − 3.0. 3 2 + 2. ( − 1 ) . − 1 2 = 1
Cho hàm số y = cos3x.sin2x. Tính y ' π 3 bằng:
A. -1
B. 1
C. - 1 2
D. 1 2
Cho hàm số y=2x^2 và y=x.Tìm toán độ giao điểm của 2 đồ thị hàm số bằng phép tính
y = 2x^2 (P) ; y = x (d)
Hoành độ giao điểm thỏa mãn phương trình
\(2x^2=x\Leftrightarrow x\left(2x-1\right)=0\Leftrightarrow x=0;x=\frac{1}{2}\)
\(\Rightarrow y=0;y=\frac{1}{2}\)
Vậy (P) cắt (d) tại O(0;0) ; A(1/2;1/2)
Xét hàm số luỹ thừa \(y = {x^\alpha }\) với \(\alpha \) là số thực.
a) Tìm tập xác định của hàm số đã cho.
b) Bằng cách viết \(y = {x^\alpha } = {e^{\alpha \ln x}}\), tính đạo hàm của hàm số đã cho.
a: Nếu a là số nguyên dương thì TXĐ là D=R
Nếu a là số không phải nguyên dương thì TXĐ là D=R\{0}
Nếu a không là số nguyên thì TXĐ: D=R
b: \(y'=\left(x^a\right)'=\left(e^{a\cdot lnx}\right)'\)
\(=\dfrac{a}{x}\cdot e^{a\cdot lnx}=\dfrac{a}{x}\cdot x^a=a\cdot x^{a-1}\)
Cho hàm số y = f ( x ) = x 4 - x 2 . Tính y'(0) bằng
A. 1 2
B. 1 3
C.1
D.2.
Chọn A
y ' = 1. 4 − x 2 − x . ( 4 − x 2 ) ' 2 4 − x 2 4 − x 2 = 4 − x 2 − x . ( − 2 x ) 2 4 − x 2 4 − x 2 = 4 − x 2 + x 2 4 − x 2 4 − x 2
⇒ y ' ( 0 ) = 2 + 0 4 − 0 = 1 2
Cho hàm số y = x 4 + a 4 + b
Tính a, b để hàm số cực trị bằng 3/2 khi x =1.
Cho hàm số y = cos 2 x 1 − sin x . Tính y ' π 6 bằng
A. y ' π 6 = 1
B. y ' π 6 = − 1
C. y ' π 6 = 3
D. y ' π 6 = − 3
Chọn D
y ' = cos 2 x ' . 1 − sin x − cos 2 x 1 − sin x ' 1 − sin x 2 = − 2 sin 2 x 1 − sin x + cos 2 x . c o s x 1 − sin x 2
y ' π 6 = − 2. 3 2 1 − 1 2 + 1 2 . 3 2 1 − 1 2 2 = − 3 2 + 3 4 1 4 = 4 − 3 2 + 3 4 = − 2 3 + 3 = − 3
Cho hàm số y = cos x 1 − sin x . Tính y ' π 6 bằng:
A. y ' π 6 = 1
B. y ' π 6 = − 1
C. y ' π 6 = 2
D. y ' π 6 = − 2
Chọn C
y ' = − sin x 1 − sin x + cos 2 x 1 − sin x 2 = − sin x + sin 2 x + cos 2 x 1 − sin x 2 = − s inx + 1 ( 1 − sin x ) 2 = 1 1 − sin x
y ' π 6 = 1 1 − sin π 6 = 2
Cho hàm số y = - x 2 + 3 x – 2 . Tính y’(2) bằng định nghĩa.
- Giả sử Δx là số gia của đối số tại xo = 2. Ta có:
Δy = y(2 + Δx) - y(2)
= -(2 + Δx)2 + 3(2 + Δx) - 2 - (-22 + 3.2 - 2)
= -(4 + 4Δx + (Δx)2 )+ 6 + 3Δx - 2 = - (Δx)2 - Δx