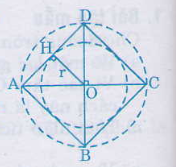
Cho hình vẽ: Hình vẽ biểu diễn:
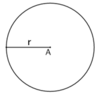
A.Đường tròn tâm O, bán kính r
B.Đường tròn tâm A, bán kính r.
C.Đường tròn O, bán kính R.
D.Đường tròn tâm A, bán kính r.
a) Vẽ đường tròn tâm O, bán kính 2cm.
b) Vẽ hình vuông nội tiếp đường tròn (O) ở câu a).
c) Tính bán kính r của đường tròn nội tiếp hình vuông ở câu b) rồi vẽ đường tròn (O; r).
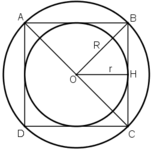
a) Chọn điểm O là tâm, mở compa có độ dài 2cm vẽ đường tròn tâm O, bán kính 2cm.
b) Vẽ đường kính AC và BD vuông góc với nhau. Nối A với B, B với C, C với D, D với A ta được tứ giác ABCD là hình vuông nội tiếp đường tròn (O; 2cm).
c) Vẽ OH ⊥ BC.
⇒ OH là khoảng cách từ từ tâm O đến BC
Vì AB = BC = CD = DA ( ABCD là hình vuông) nên khoảng cách từ tâm O đến AB, BC, CD, DA bằng nhau ( định lý lien hệ giữa dây cung và khoảng cách từ tâm đến dây)
⇒ O là tâm đường tròn nội tiếp hình vuông ABCD
OH là bán kính r của đường tròn nội tiếp hình vuông ABCD.
Tam giác vuông OBC có OH là đường trung tuyến ⇒ 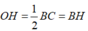
Xét tam giác vuông OHB có: r 2 + r 2 = O B 2 = 2 2 ⇒ 2 r 2 = 4 ⇒ r 2 = 2 ⇒ r = 2 ( cm )
Vẽ đường tròn (O; OH). Đường tròn này nội tiếp hình vuông, tiếp xúc bốn cạnh hình vuông tại các trung điểm của mỗi cạnh.
Kiến thức áp dụng
+ Đường tròn ngoại tiếp đa giác nếu đường tròn đó đi qua tất cả các đỉnh của đa giác. Khi đó ta nói đa giác nội tiếp đường tròn.
+ Đường tròn nội tiếp đa giác là đường tròn tiếp xúc với tất cả các cạnh của đa giác. Khi đó ta nói đa giác ngoại tiếp đường tròn.
cho góc xOy và tia Am
vẽ cng tròn tâm O bán kính r , cung này cắt Ox và Oy ở B và C .Vẽ cung tròn tâm A bán kính r , cung này cắt tia Am tại D . Vẽ cung tròn tâm D bán kính BC , cung này cắt cung tròn tâm A bán kính r tại E . CMR GÓC DAE = GÓC xOy
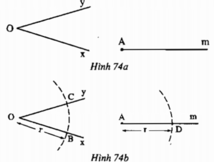
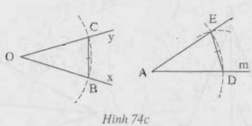
Cho góc xOy và tia Am ( h.74a).
Vẽ cung tròn tâm O bán kính r, cung này cắt Ox, Oy theo thứ tự ở B, C. Vẽ cung tròn tâm A bán kính r, cung này cắt tia Am ở D (h.74b).Vẽ cung tròn tâm D có bán kính bằng BC, cung này cắt cung tròn tâm A, bán kính r ở E (h.74c).
Chứng minh rằng góc DAE = góc xOy
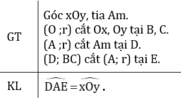
Kí hiệu: (O ;r) là đường tròn tâm O bán kính r.
B, C thuộc (O; r) nên OB = OC = r.
D thuộc (A;r) nên AD = r.
E thuộc (D; BC) và (A;r) nên AE = r, DE = BC.
Xét OBC và ADE có:
OB = AD (cùng bằng r)
OC = AE (cùng bằng r)
BC = DE
Nên ΔOBC = ΔADE (c.c.c)
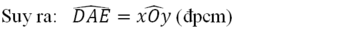
a) Vẽ đường tròn tâm O, bán kính 2cm.
b) Vẽ hình vuông nội tiếp đường tròn (O) ở câu a.
c) Tính bán kính r của đường tròn nội tiếp hình vuông ở câu b) rồi vẽ đường tròn (O; r).
a) Chọn điểm O làm tâm , mở compa có độ dài 2cm vẽ đường tròn tâm O, bán kính 2cm: (O; 2cm)
Vẽ bằng eke và thước thẳng.
b) Vẽ đường kính AC và BD vuông góc với nhau. Nối A với B, B với C, C với D, D với A ta được tứ giác ABCD là hình vuông nội tiếp đường tròn (O;2cm)
c) Vẽ OH ⊥ AD
OH là bán kính r của đường tròn nội tiếp hình vuông ABCD.
r = OH = AH.
r2 + r2 = OA2 = 22 => 2r2 = 4 => r = √2 (cm)
Vẽ đường tròn (O;√2cm). Đường tròn này nội tiếp hình vuông, tiếp xúc bốn cạnh hình vuông tại các trung điểm của mỗi cạnh
cho góc xOy và tia Am
Vẽ cung tròn tâm O bán kính r,cung này cắt Ox,Oy theo thứ tự ở B,C.Vẽ cung tròn tâm A bán kính r,cung nàycắt Am ở D
Vẽ cung tròn tâm D có bán kính bằng BC,cung này cắt cung tròn tâm A bán kính r ở E
Chứng minh rằng góc DAE=xOy
Cho góc xOy và tia Am
Vẽ cung tròn tâm O bán kính r, cung này cắt Ox, Oy theo thứ tự ở B, C. Vẽ cung tròn tâm A bán kính r, cung này cắt tia Am ở D
Vẽ cung tròn tâm D có bán kính bằng BC, cung này cắt cung tròn tâm A bán kính r ở E.
Chứng minh rằng góc DAE = góc xOy.
cho góc xoy và tia Am
vẽ cung tròn tâm O bán kính r,cung này cắt ox,oy theo thứ tự ở B,C . vẽ cung tròn tâm A bán kính r,cung này cắt tia Am ở D
vẽ cung tròn tâm D có bán kính bằng BC,cung này cắt cung tròn tâm A bán kính r ở E
Cm rằng góc DAE=góc xoy
Cho đường tròn tâm O bán kính R có đường kính AB cố định. Vẽ đường kính MN của đường tròn tâm O bán kính R (M khác A ,M khác B). Tiếp tuyến của dường tròn tâm o bán kính r tại B cắt đường thẳng AM AN lần lượt tại Q và P
a, Cm tg AMNB Là hình chữ nhật
b, chứng minh 4 điểm M, N, P, Q cùng thuộc 1 đường tròn
Cho góc xOy và tia Am
Vẽ cung tròn tâm O bán kính r,cung này cắt Ox,Oy theo thứ tự ở B,C.Vẽ cung tròn tâm A bán kính r,cung này cắt tia Am ở D.
Vẽ cung tròn tâm D có bán kính bằng BC,cung này cắt cung tròn tâm A bán kính r ở E
Chứng minh rằng góc DAE=góc xOy
Xét tam giác OBC và tam giác AED có
OB = AE (GT)
OC = AD (GT)
BC = ED (GT)
=> tam giác OBC = tam giác AED
=> góc xOy = góc DAE (2 góc tương ứng)
Vậy góc xOy = góc DAE
Cho một điểm M thuộc đường tròn tâm O đường kính R. Vẽ đường tròn tâm O' bán kính r có đường kính OM. Một bán kính OA của đường tròn (O) cắt đường tròn (O') ở B.
a) Chứng minh cung MA và cung MB có độ dài bằng nhau.
b) Biết góc AOM = 450 và R = 10cm. Tính diện tích giới hạn bởi cung MA, cung MB và đoạn AB.