Cho đường thẳng d có phương trình m - 1 2 x + ( 1 – 2 m ) y = 2 . Tìm các giá trị của tham số m để d song song với trục tung.
A. m = 1
B. m ≠ 1 2
C. m = 2
D. m = 1 2
Cho đường thẳng (d) có phương trình: x- 2y+ 5= 0. Có mấy phương trình đường thẳng qua M(2; 1) và tạo với d một góc 450.
A. 1
B. 2
C. 3
D. Không có.
Đáp án B
Gọi ∆ là đường thẳng cần tìm và n → ( A ; B ) là VTPT của ∆ A 2 + B 2 ≠ 0
Để ∆ tạo với đường thẳng ( d) một góc 450 thì:
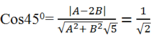
Tương đương: 2( A- 2B) 2= 5( A2+ B2)
Nên A= -3B hoặc B= 3A
+ Với A= - 3B, chọn B= -1 thì A= 3 ta được phương trình ∆ : 3x- y- 5= 0.
+ Với B= 3A, chọn A= 1 thì B= 3 ta được phương trình ∆: x+ 3y- 5 = 0 .
Trong mặt phẳng tọa độ Oxy, cho parabol (P) có phương trình và đường thẳng (d) có phương trình
1, trong đó m là tham số.
a, Vẽ parabol (P).
b, Xác định m để đường thẳng (d) cắt (P) tại hai điểm phân biệt.
c, Chứng minh rằng khi m thay đổi, các đường thẳng (d) luôn đi qua một điểm cố định Trong mặt phẳng tọa độ Oxy, cho parabol (P) có phương trình
và đường thẳng (d) có phương trình
1, trong đó m là tham số.
a, Vẽ parabol (P).
b, Xác định m để đường thẳng (d) cắt (P) tại hai điểm phân biệt.
c, Chứng minh rằng khi m thay đổi, các đường thẳng (d) luôn đi qua một điểm cố định
a:
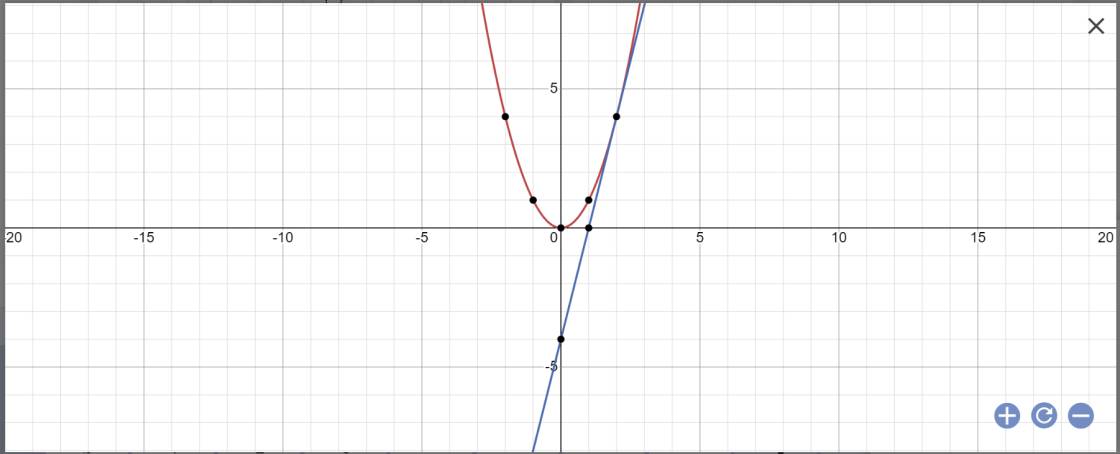
b: PTHĐGĐ là:
2x^2-(2m-2)x+m-1=0
Δ=(2m-2)^2-4*2*(m-1)
=4m^2-8m+4-8m+8
=4m^2-16m+12
=4m^2-2*2m*4+16-4=(2m-4)^2-4=(2m-6)(2m-2)
Để (d) cắt (P) tại 2 điểm pb thì (2m-6)(2m-2)>0
=>m>3 hoặc m<1
Cho mặt phẳng (α) có phương trình: 3x + 5y - z - 2 = 0 và đường thẳng d có phương trình: x = 12 + 4 t y = 9 + 3 t z = 1 + t
Viết phương trình mặt phẳng β chứa điểm M và vuông góc với đường thẳng d.
(β) vuông góc với d
⇒ (β) nhận vtcp của d 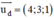 là 1 vtpt.
là 1 vtpt.
(β) đi qua M(0; 0; -2)
⇒ (β): 4x + 3y + z + 2 = 0.
Cho mặt phẳng (α) có phương trình: 3x + 5y - z - 2 = 0 và đường thẳng d có phương trình: x = 12 + 4 t y = 9 + 3 t z = 1 + t
Tìm giao điểm M của đường thẳng d và mặt phẳng α .
M ∈ d ⇒ M(12 + 4t; 9 +3t; 1 + t).
M ∈ α ⇒ 3.(12 + 4t) + 5.(9 + 3t) – (1 + t) – 2 = 0
⇔ 26t + 78 = 0.
⇔ t = -3.
⇒ M(0; 0; -2).
d) Tìm a, b để đồ thị hàm số đi qua điểm A(1; 2) và B(2;1)
e) Lập phương trình đường thẳng đi qua gốc toạ độ O và điểm A(1; 2)
f) Lập phương trình đường thẳng (d) đi qua M(2; -1) và vuông góc với đường thẳng (d’) có phương trình: y = −1 2 x +3
Cho đường thẳng (d) có phương trình y= (m-1)x+2 (m là hàm số). xác định m để khoảng cách từ gốc tọa độ đến đường thẳng (d) là xa nhất
Trong không gian với hệ tọa độ Oxyz, cho điểm M(2;1;0) và đường thẳng d có phương trình d : x - 1 2 = y + 1 1 = z - 1 Phương trình của đường thẳng ∆ đi qua điểm, M cắt và vuông góc với đường thẳng d là:
A. x - 2 1 = y - 1 - 4 = z - 2
B. x - 2 - 1 = y - 1 - 4 = z 2
C. x - 2 - 1 = y - 1 - 3 = z 2
D. x - 2 - 3 = - y - 1 - 4 = z - 2
cho đường thẳng (d) : x - 2y + 1 = 0. nếu đường thẳng (Δ) đi qua M(1;-1) và song song với (d) thì (Δ) có phương trình ?
\(\Delta\) đi qua M(1,-1) có hệ số góc k
=> \(\Delta:y=k\left(x-1\right)-1=kx-k-1\)
\(\Delta\) song song d: \(y=\dfrac{1}{2}x+\dfrac{1}{2}\) \(=>k=\dfrac{1}{2}\)
\(\Delta:y=\dfrac{1}{2}x-\dfrac{3}{2}\)
Cho đường thẳng y=(D1) có phương trình y= x+2, (D2) có phương trình y= -2x+8 ,(D3) có phương trình (m+1)x -m. Tìm m để 3đường thẳng đồng quy.
Gọi A là giao điểm của (D1) và (D2).
Phương trình hoành độ giao điểm của (D1) và D(2)
x + 2 = -2x + 8
--> x = 2
Thay vào (D1) hoặc (D2) tính được y = 4
Để 3 đường thẳng đồng quy, chứng minh điểm A thuộc đường thẳng D(3)
Thay toa độ điểm A vào pt đường thẳng (D3)
4 = (m + 1) . 2 - m
4 = 2m + 2 - m
2 = m
Vậy phương trình đường thẳng (D3) y = 3x - 2 thì ba đường thẳng đồng quy tại A (2; 4)
cho đường thẳng (d) có phương trình y = (2m - 1)x + m + 1 và đường thẳng (d') có phương trình y = x+ 3
a, tính giá trị của m để đường thẳng (d) cắt đường thẳng (d') tại một điểm trên trục tung
b, tìm m để khoản cách từ gốc tọa độ O đến dường thẳng (d) đạt giá trị lớn nhất và giá trị lớn nhất đó bằng nhau