a: góc AMC=1/2*180=90 độ

=>góc DMC=90 độ

góc CNB=1/2*180=90 độ

=>góc DNC=90 độ

Kẻ tiếp tuyến Cx của hai đường tròn đường kính AC,CB, Cx cắt MN tại I

Xét (E) có

IC,IM là tiếp tuyến

=>IC=IM

Xét (F) có

IN,IC là tiếp tuyến

=>IN=IC=IM

Xét ΔMCN có

CI là trung tuyến

CI=MN/2

=>ΔMCN vuông tại C

góc DMC=góc DNC=góc MCN=90 độ

=>DMCN là hcn

b: ΔDCA vuông tại C có CM vừa là đường cao

nên DM*DA=DC^2

ΔDCB vuông tại C có CN là đường cao

nên DN*DB=DC^2=DM*DA

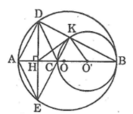
Tam giác ABD nội tiếp trong đường tròn (O) có Ab là đường kính nên vuông tại D

Suy ra: AD ⊥ BD

Tứ giác ADCE là hình thoi nên EC // AD

Suy ra: EC ⊥ BD     (1)

Tam giác BCK nội tiếp trong đường tròn (O’) có BC là đường kính nên vuông tại K

Suy ra: CK ⊥ BD     (2)

Từ (1) và (2) suy ra EC trùng với CK

Vậy E, C, K thẳng hàng.

Câu 1:

Gọi giao điểm của OC với AB là H

Vì OC\(\perp\)AB nên OH\(\perp\)AB tại H

=>OH là khoảng cách từ O xuống dây AB

Ta có: ΔOAB cân tại O

mà OH là đường cao

nên H là trung điểm của AB

=>HA=HB=AB/2=8(cm)

ΔOHA vuông tại H

=>\(OH^2+HA^2=OA^2\)

=>\(OH^2=10^2-8^2=36\)

=>\(OH=\sqrt{36}=6\left(cm\right)\)

Câu 2:

a: Xét (O) có

AB là đường kính

BC là dây

Do đó: AB>BC

b: Xét (O) có

ΔCAB nội tiếp

AB là đường kính

Do đó: ΔCAB vuông tại C

c: Xét ΔACB có

O là trung điểm của AB

OM//CB

Do đó: M là trung điểm của AC

Khá khó nên gạch xóa hơi nhiều

Link ảnh: https://imgur.com/a/cE1k5pV

thêm playing

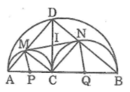
Gọi P là trung điểm của AC, Q là trung điểm của BC, I là giao điểm của MN với DC

Vì CMDN là hình chữ nhật nên IC = IM = ID = IN

Tam giác CNI cân tại I nên  (3)

Tam giác CNQ cân tại Q nên      (4)

Vì AB ⊥ CD nên  = 90 °    (5)

Từ (3), (4) và (5) suy ra:  =  90 °  hay MN ⊥ QN

Vậy MN là tiếp tuyến của đường tròn đường kính BC

Tam giác CMI cân tại I nên 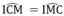     (6)

Tam giác CMP cân tại P nên 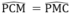     (7)

Vì AB ⊥ CD nên 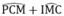 =  90 °     (8)

Từ (6), (7) và (8) suy ra: 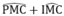 =  90 °  hay MN ⊥ PM

Vậy MN là tiếp tuyến của đường tròn đường kính AC