Cho đoạn thẳng AB, điểm C nằm giữa AB. Vẽ về một phía của AB các nửa đường tròn có đường kính theo thứ tự là AB, AC, BC. Đường vuông góc với AB tại C cắt nửa đường tròn lớn hơn tại D. DA, DB cắt các nửa đường tròn có đường kính AC, BC theo thứ tự tại M, N. Chứng minh rằng MN là tiếp tuyến chung của các nửa đường tròn có đường kính AC, BC
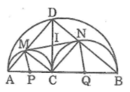
Gọi P là trung điểm của AC, Q là trung điểm của BC, I là giao điểm của MN với DC
Vì CMDN là hình chữ nhật nên IC = IM = ID = IN
Tam giác CNI cân tại I nên 
(3)
Tam giác CNQ cân tại Q nên 
(4)
Vì AB ⊥ CD nên 
=
90
°
(5)
Từ (3), (4) và (5) suy ra: 
=
90
°
hay MN ⊥ QN
Vậy MN là tiếp tuyến của đường tròn đường kính BC
Tam giác CMI cân tại I nên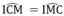 
(6)
Tam giác CMP cân tại P nên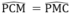 
(7)
Vì AB ⊥ CD nên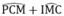 
=
90
°
(8)
Từ (6), (7) và (8) suy ra: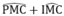 
=
90
°
hay MN ⊥ PM
Vậy MN là tiếp tuyến của đường tròn đường kính AC
