Đồ thị hàm số y = x 4 - 2 m x 2 + 2 m có ba điểm cực trị tạo thành ba đỉnh của một tam giác đều khi:
A. 
B. 
C. 
D. 
Cho hàm số y = x 4 - 2 x 2 + 1 có đồ thị (C) Biết rằng đồ thị (C) có ba điểm cực trị tạo thành ba đỉnh của một tam giác, gọi là △ A B C .Tính diện tích △ A B C
A. S = 2
B. S = 1
C. S = 1 2
D. S = 4
Cho hàm số y = x 4 - 2 m x 2 - m . Với giá trị nào của m thì đồ thị hàm số có 3 điểm cực trị đồng thời ba điểm cực trị đó tạo thành một tam giác vuông cân.
A. m = -1
B. m = 0
C. m = 1
D. m = 2 3
Đáp án C
Tập xác định D = R
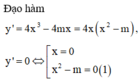
Đồ thị hàm số có 3 điểm cực trị Û y’ = 0 có ba nghiệm phân biệt Û (1) có hai nghiệm phân biệt khác 0 Û m > 0
Với m > 0, các điểm cực trị đó là
khi đó tam giác ABC là tam giác cân đỉnh A
Để tam giác ABC là tam giác vuông cân
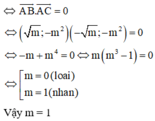
Cho hàm số y = x 4 - 2 m x 2 - m . Với giá trị nào của m thì đồ thị hàm số có 3 điểm cực trị đồng thời ba điểm cực trị đó tạo thành một tam giác vuông cân.
A. m = -1
B. m = 0
C. m = 1
D. m = 2 3
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = x 4 - 4 m - 1 2 + 2 m - 1 có 3 điểm cực trị tạo thành 3 đỉnh của một tam giác đều.
A. 
B.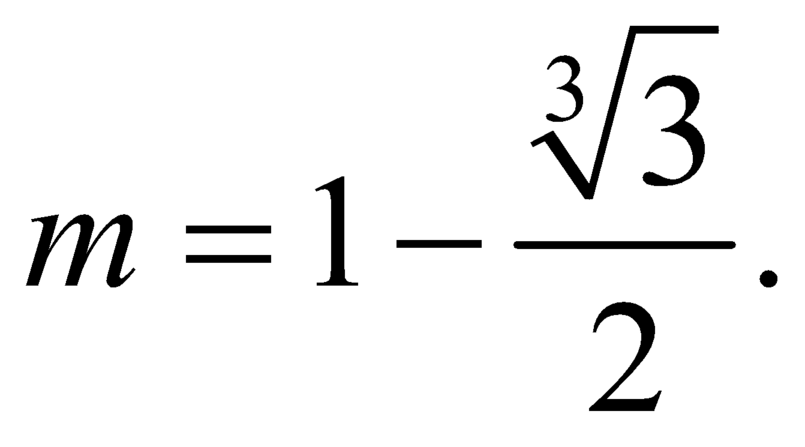 
C. 
D. 
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = x 4 - 4 m - 1 x 2 + 2 m - 1 có 3 điểm cực trị tạo thành 3 đỉnh của một tam giác đều.
A. m = 1 + 3 3 2
B. m = 1 - 3 3 2
C. m=0
D. m=1
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = x 4 - 4 ( m - 1 ) x 2 + 2 m - 1 có 3 điểm cực trị tạo thành 3 đỉnh của một tam giác đều
A. m = 0
B. m = 1
C. m = 1 + 3 3 2
D. m = 1 - 3 3 2
Chọn C
Ta có
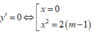nên hàm số có 3 điểm cực trị khi m > 1.
Với đk m > 1 đồ thị hàm số có 3 điểm cực trị là:
Ta có:
Để 3 điểm cực trị của đồ thị hàm số tạo thành tam giác đều thì:
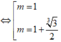
So sánh với điều kiện ta có: m = 1 + 3 3 2 thỏa mãn.
[Phương pháp trắc nghiệm]
Yêu cầu bài toán
Tìm các giá trị của tham số m để đồ thị hàm số: y = x 4 - 2 m x 2 + 2 m + m 4 có ba điểm cực trị là ba đỉnh của một tam giác đều
A. Không tồn tại m
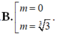
C. m = 3 3 .
D. m = ± 3 .
Chọn C
Hàm số có 3 cực trị ⇔ m > 0
Khi đó 3 điểm cực trị của đồ thị hàm số là
Do tính chất đối xứng, ta có ∆ A B C cân tại đỉnh A
Vậy ∆ A B C đều chỉ cần AB = BC
Kết hợp điều kiện ta có m = 3 3 (thỏa mãn)
Lưu ý: có thể sử dụng công thức b 3 8 a + 3 = 0
( - 2 m ) 3 8 + 3 = 0 ⇔ m 3 = 3 m ⇔ m = 3 3
Có giá trị của tham số m để đồ thị hàm số y= x4-4( m-1) x2+2m-1 có 3 điểm cực trị tạo thành 3 đỉnh của một tam giác đều. Hỏi số nguyên nào gần với số m nhất?
A. 2
B. 3
C. 4
D. đáp án khác
Ta có đao hàm y’ = 4x3- 8( m-1) x= 4x( x2- 2( m-1) )
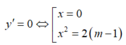
nên hàm số có 3 điểm cực trị khi m> 1.
Với điều kiện m > 1 đồ thị hàm số có 3 điểm cực trị là:
A ( 0 ; 2 m - 1 ) , B ( 2 ( m - 1 ) ; - 4 m 2 + 10 m - 5 ) , C ( - 2 ( m - 1 ) ; - 4 m 2 + 10 m - 5 ) .
Ta có: AB2= AC2= 2( m-1) + 16( m-1) 4; BC2= 8( m-1)
Để 3 điểm cực trị của đồ thị hàm số tạo thành tam giác đều thì:
AB= AC= BC tương đương AB2= AC2= BC2
Do đó: 2( m-1) + 16( m-1) 4= 8( m-1)
⇔ 8 ( m - 1 ) 4 - 3 ( m - 1 ) = 0
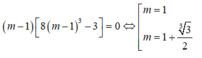
So sánh với điều kiện ta có: m = 1 + 3 3 2 thỏa mãn.
Chọn A.
0 <=> m>0
