Trong mặt phẳng Oxy, thực hiện liên tiếp phép đối xứng tâm O và phép quay tâm O góc quay 90 o biến đường thẳng y = x + 1 thành đường thẳng
A. x - y - 1 = 0
B. -x + y - 1 = 0
C. x + y + 1 = 0
D. x + y - 1 = 0
Trong mặt phẳng Oxy cho đường thẳng d có phương trình 3x – y – 3 = 0. Viết phương trình đường thẳng d 1 là ảnh của d qua phép dời hình có được bằng cách thực hiện liên tiếp phép đối xứng tâm I(−1;2) và phép quay tâm O góc quay - 90 ο .
Giả sử M 1 = D I ( M ) và M ′ = Q O ; − 90 ο ( M 1 ) . Ta có
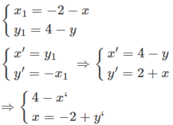
Thế (x;y) theo (x′;y′) vào phương trình d ta có:
3(y′ − 2) − (4 − x′) – 3 = 0 ⇔ x′ + 3y′ − 13 = 0
Vậy phương trình d’ là x + 3y – 13 = 0.
Trong mặt phẳng Oxy, thực hiện liên tiếp phép đối xứng trục Oy và phép quay tâm O góc quay 90 ° biến điểm M (1;1) thành điểm M''. Tọa độ M'' là:
A. - 1 ; 1 .
B. - 1 ; - 1 .
C. 1 ; - 1 .
D. - 2 ; - 2
Trong mặt phẳng với hệ tọa độ Oxy cho đường thẳng d có phương trình x+2y+3=0. Viết phương trình đường thẳng d’ là ảnh của d qua phép đồng dạng có được từ việc thực hiện liên tiếp phép quay tâm O góc quay - 90 ∘ và phép vị tự tâm O tỉ số 5.
A. d' : 2x-y-15=0
B. d' : 2x-y+15=0
C. d' : 2x-y+ 3 5 =0
B. d' : x-y+30=0
Trong mặt phẳng với hệ tọa độ Oxy cho đường thẳng d có phương trình x + 2 y + 3 = 0 . Viết phương trình đường thẳng d’ là ảnh của d qua phép đồng dạng có được từ việc thực hiện liên tiếp phép quay tâm O góc quay − 90 ° và phép vị tự tâm O tỉ số 5.
A. d ' : 2 x − y − 15 = 0
B. d ' : 2 x − y + 15 = 0
C. d ' : 2 x − y + 3 5 = 0
D. d ' : x + 2 y − 30 = 0
Đáp án B
d cắt Ox,Oy lần lượt tại A − 3 ; 0 ; B 0 ; − 3 2 Qua phép quay tâm O góc quay − 90 ° điểm A và B lần lượt biến thành các điểm A ' 0 ; 3 ; B − 3 2 ; 0 ⇒ A ' B ' : 2 x − y + 3 = 0
Phép vị tự biến đường thẳng thành đường thẳng song song với nó nên d ' : 2 x − y + m = 0
Qua V O ; k A ' = A 1 ⇒ O A 1 → = 5 O A ' → ⇒ A 1 0 ; 15 ⇒ d ' : 2 x − y + 15 = 0
Trong mặt phẳng Oxy, thực hiện liên tiếp phép quay tâm O góc quay - 45 o và phép đối xứng tâm O thì điểm M(1;1) biến thành điểm M’’ có tọa độ là:
A. (-1;0)
B. (√2;0)
C. (√2;-√2)
D. (-√2;0)
+) Phép quay tâm O góc quay − 45 ° biến điểm M(x; y) thành điểm M’(x’;y’) với biểu thức tọa độ là:
Với M(1; 1) suy ra tọa độ điểm M’ là x ' = x cos − 45 ° − y sin − 45 ° y ' = x sin − 45 ° + y cos − 45 ° ⇔ x ' = 2 2 x + 2 2 y y ' = − 2 2 x + 2 2 y
+) Phép đối xứng tâm O biến điểm M’ thành M’’ x ' = 2 2 .1 + 2 2 .1 = 2 y ' = − 2 2 .1 + 2 2 .1 = 0 ⇒ M ' 2 ; 0
Suy ra tọa độ M ' ' − 2 ; 0
Đáp án D
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): x - 1 2 + y - 2 2 = 4 . Phép đồng dạng thực hiện bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số k= - 2 và phép quay tâm O góc quay 180 ∘ , khi đó đường tròn (C) sẽ biến thành đường tròn nào sau đây
A. x 2 + y 2 - 4 x - 8 y - 2 = 0
B. x 2 + y 2 + 4 x + 8 y + 2 = 0
C. x + 2 2 + y + 4 2 = 16
D. x - 2 2 + y - 4 2 = 16
Trong mặt phẳng Oxy cho đường thẳng d có phương trình x+y-2=0. Viết phương trình đường thẳng d’ là ảnh của d qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm I ( - 1 ; - 1 ) tỉ số k= 1 2 và phép quay tâm O góc - 45 ∘
A. y=0
B. y=-x
C. y=x
D. x=0
Trong mặt phẳng Oxy cho đường thẳng d có phương trình x + y − 2 = 0 . Viết phương trình đường thẳng d’ là ảnh của d qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm I − 1 ; − 1 tỉ số k = 1 2 và phép quay tâm O góc − 45 °
A. y=0
B. y= -x
C. y=x
D.x=0
Đáp án D
Ta có V I , 1 2 biến M 0 ; 2 ∈ d thành M ' x ' ; y ' thì I M ' → = 1 2 I M → ⇔ x ' = − 1 2 y ' = 1 2
V I , 1 2 biến đường thẳng d thành đường thẳng đi qua M ' − 1 2 ; 1 2 , có cùng vtpt 1 ; 1 và có phương trình là x + 1 2 + y − 1 2 = 0 ⇔ x + y = 0
Phép quay tâm O góc quay − 45 ° biến điểm N x ; y thuộc đường thẳng x + y = 0 thành điểm
N ' x ' ; y ' ∈ d ' ⇒ x = x ' cos 45 ° − y ' sin 45 ° y = x ' sin 45 ° + y ' cos 45 ° ⇒ x = 2 2 x ' − y ' y = 2 2 x ' + y ' *
Thay (*) vào x + y = 0 ta được x ' = 0 ⇒ d ' : x = 0
Trong mặt phẳng Oxy cho đường thẳng d có phương trình x + y − 2 = 0 . Viết phương trình đường thẳng d’ là ảnh của d qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm I − 1 ; − 1 tỉ số k = 1 2 và phép quay tâm O góc − 45 °
A.y=0
B. y=-x
C. y=x
D. x=0
Đáp án D
Ta có V I , 1 2 biến M 0 ; 2 ∈ d thành M ' x ' ; y ' thì I M ' → = 1 2 I M → ⇔ x ' = − 1 2 y ' = 1 2
V I , 1 2 biến đường thẳng d thành đường thẳng đi qua M ' − 1 2 ; 1 2 , có cùng vtpt 1 ; 1 và có phương trình là x + 1 2 + y − 1 2 = 0 ⇔ x + y = 0
Phép quay tâm O góc quay − 45 ° biến điểm N x ; y thuộc đường thẳng x + y = 0 thành điểm
N ' x ' ; y ' ∈ d ' ⇒ x = x ' cos 45 ° − y ' sin 45 ° y = x ' sin 45 ° + y ' cos 45 ° ⇒ x = 2 2 x ' − y ' y = 2 2 x ' + y ' *
Thay * vào x + y = 0 ta được x ' = 0 ⇒ d ' : x = 0