Cho hình chóp S.ABC có AB=2a, BC = a, A B C ^ = 120 o Biết mặt phẳng (SAC) vuông góc với mặt phẳng (ABC), d(C,SA)=2. Côsin góc giữa hai mặt phẳng (SAC) và (SAB) bằng
A. 777 37
B. 4 37 37
C. 21 10
D. 10 11 .
Cho hình chóp S.ABC có SA vuông góc với đáy, S A = a 3 , A B = a , B C = 2 a , A C = a 5 . Tính thể tích khối chóp S.ABC theo a.
A. 2 a 3 3
B. 2 a 3 3 3
C. a 3 3
D. a 3 3
Chọn B.
Phương pháp
Tính diện tích đáy và chiều cao rồi áp dụng công thức V = 1 3 S h tính thể tích.
Cách giải:
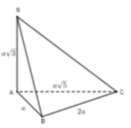

Cho hình chóp S.ABC có SA vuông góc với đáy, S A = a 3 , A B = a , B C = 2 a , A C = a 5 . Tính thể tích khối chóp S.ABC theo a.
![]()
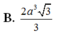
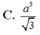
![]()
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B có AB=BC=a,SB=2a và SA vuông góc với đáy. Tính thể tích khối chóp S.ABC.
Cho hình chóp S.ABC có đáy là tam giác vuông tại B, AB=a, BC=2a. SA vuông góc với đáy. Thể tích của khối chóp S.ABC bằng a 3 2 . Tính chiều cao h của khối chóp đã cho
A. h = 3 a 2
B. h = a 2
C. h = a 2
D. h = 2 a 3
Đáp án A
Diện tích đáy là:
S d = B A . B C 2 = a 2 ⇒ h = 3 V S = 3 a 2
Cho khối chóp S.ABC có SA⊥ AB, AB ⊥ BC, BC ⊥ SC, AB = 2a, BC = a, A S C ^ = 60 ° Thể tích khối chóp S.ABC bằng
A. 2 a 3 12
B. 2 73 - 30 a 3 9
C. 30 + 6 73 a 3 18
D. 2 a 3 6
Gọi D=h/c(S,(ABC)) ta có 
![]()
Có 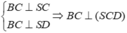 ⇒
B
C
⊥
C
D
Và
A
B
C
^
=
90
°
kết hợp lại có ABCD là hình chữ nhật.
⇒
B
C
⊥
C
D
Và
A
B
C
^
=
90
°
kết hợp lại có ABCD là hình chữ nhật.
Đặt SD = h, theo pitago có
![]()
![]()
![]()
Vì
![]()
![]()


Vậy
![]()
![]()

Chọn đáp án C.
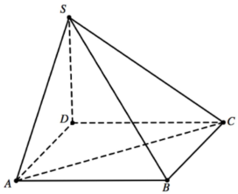
Cho hình chóp S.ABC có đáy ABC là tam giác cân tại B, AB=BC=a và ∠ A B C = 120 ° . Cạnh bên SA vuông góc với mặt phẳng đáy và SA=2a. Tính theo a bán kính mặt cầu ngoại tiếp hình chóp S.ABC.
A. a 2 5
B. a 2
C. a 5
D. a 2 4
Đáp án B.
Dựng tam giác đều IAB (I và C cùng phía bờ AB).
Ta có:
Qua I dựng đường thẳng song song với SA, cắt đường trung trực của SA tại O thì O là tâm mặt cầu ngoại tiếp hình chóp.
Gọi M là trung điểm của SA.
Ta có:
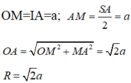
Cho hình chóp S.ABC có đáy ABC là tam giác cân tại B, AB=BC=a và ∠ A B C = 120 ° . Cạnh bên SA vuông góc với mặt phẳng đáy và SA=2a. Tính theo a bán kính mặt cầu ngoại tiếp hình chóp S.ABC
A. a 2 5
B. a 2
C. a 5
D. a 2 4
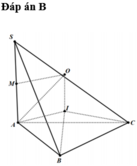
Dựng tam giác đều IAB (I và C cùng phía bờ AB). Ta có ∠ I B C = 120 ° - 60 ° = 60 ° và IB=BC nên DIBC đều, IA=IB=IC=a
Qua I dựng đường thẳng song song với SA, cắt đường trung trực của SA tại O thì O là tâm mặt cầu ngoại tiếp hình chóp.
Gọi M là trung điểm của SA.
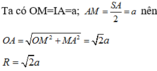
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB = a, BC = 2a, cạnh bên SA vuông góc với đáy và S A = a 3 . Tính diện tích S m c của mặt cầu ngoại tiếp hình chóp S.ABC
A. S m c = 4 πa 2
B. S m c = 32 πa 2
C. S m c = 8 πa 2
D. S m c = 16 πa 2
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB = a, BC = 2a, cạnh bên SA vuông góc với đáy và SA = a 3 .Tính diện tích S m c của mặt cầu ngoại tiếp hình chóp S.ABC.
![]()
![]()
![]()
![]()
Cho hình chóp S.ABC có S A ⊥ A B C , tam giác ABC vuông tại B. Biết S A = 2 a , A B = a , B C = a 3 . Tính bán kính R của mặt cầu ngoại tiếp hình chóp
A. a
B. 2a
C. a 2
D. 2 a 2