Cho số phức z thỏa mãn điều kiện ( 3 + 2 i ) z + ( 2 - i ) 2 = 4 + i . Tìm phần ảo của số phức w = ( 1 + z ) z ¯ .
![]()
![]()
![]()
![]()
Cho số phức z thỏa mãn điều kiện ( 3 + 2 i ) z + ( 2 - i ) 2 = 4 + i . Tìm phần ảo của số phức w = ( 1 + + z ) z ¯ .
A. -2
B. 0.
C. -1
D. 1
Cho số phức z thỏa mãn điều kiện z - 3 + 2 i = z - i Giả sử w là số phức có môđun nhỏ nhất trong các số phức z thỏa mãn điều kiện trên. Tính môđun của w
![]()
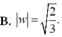
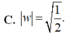
![]()
Cho số phức z thỏa mãn điều kiện z - 1 = 2 . Tìm giá trị lớn nhất của T = z + i + z - 2 - i
A. m a x T = 8 2
B. m a x T = 4
C. m a x T = 4 2
D. m a x T = 8 2
Cho số phức z thỏa mãn điều kiện (1 - i)(2 + i)z + 1 - i = (5 - i)(1 + i). Tính môđun của số phức w = 1 + 2 z + z 2
A. 8
B. 64
C. 2 2
D. 5
Đáp án A
Ta có z = 5 - i 1 + i + i - 1 1 - i 2 + i = 1 + 2 i ⇒ w = 8 i ⇒ w = 8 .
Cho số phức z thỏa mãn điều kiện z - 1 = 2 . Tìm giá trị lớn nhất của biểu thức T = z + i + z - 2 - i
![]()
![]()
![]()
![]()
Tập hợp các điểm z thỏa mãn điều kiện z - 1 = 2 là đường tròn (C) tâm I(1;0) bán kính R = 2
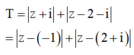
Gọi M là điểm biểu diễn cho số phức z, A(0,-1) là điểm biểu diễn cho số phức -i, B(2;1)là điểm biểu diễn cho số phức 2+i

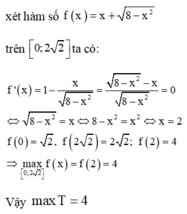
Đáp án D
Cho số phức z thỏa mãn điều kiện z - 1 = 2 .
Tìm giá trị lớn nhất của biểu thức T = z + i + z - 2 - i
A. maxT= 8 2
B. maxT=8
C. maxT= 4 2
D. maxT=4
Đáp án D
Phương pháp: Đưa biểu thức T về dạng biểu thức vector bằng cách tìm các vecto biểu diễn cho các số phức.
Cách giải:
Tập hợp các điểm z thỏa mãn điều kiện ![]() là đường tròn (C) tâm I(1;0) bán kính R=
2
là đường tròn (C) tâm I(1;0) bán kính R=
2
![]()
Gọi M là điểm biểu diễn cho số phức z, A(0;-1) là điểm biểu diễn cho số phức -i, B(2;1) là điểm biểu diễn cho số phức 2+i
Dễ thấy A,B
∈
C và ![]()
![]() AB là đường kính của đường tròn (C)
AB là đường kính của đường tròn (C)
![]() vuông tại M
vuông tại M
![]()
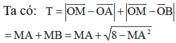
Đặt ![]()
Xét hàm số ![]() trên
trên ![]() ta có:
ta có:
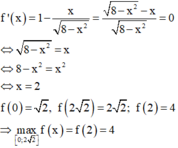
Vậy maxT=4
Biết số phức z thỏa mãn đồng thời hai điều kiện z - 3 - 4 i = 5 và biểu thức M = | z + 2 | 2 - | z - i | 2 đạt giá tri lớn nhất. Tính môđun của số phức z+i
![]()
![]()
![]()
![]()
Có bao nhiêu số phức z thỏa mãn các điều kiện z - 2 + i = 2 v à ( z + i ) 2 là số thuần ảo?
![]()
![]()
![]()
![]()
Cho số phức z thỏa mãn điều kiện \(2\left(z+1\right)=3\overline{z}+i\left(5-i\right)\). Tính Môdun của z
Giả sử: \(z=x+yi (x;y\in |R)\)
Ta có: \(2(z+1)=3\overline{z}+i(5-i) \)
<=>\(2(x+yi+1)=3(x-yi)+i(5-i)\)
<=>\(2x+2yi+2=3x-3yi+5i-i^2\)
<=>\((3x-2x+1-2)+(5-3y-2y)i=0\)
<=>\((x-1)+(5-5y)i=0\)
<=>\(\begin{align} \begin{cases} x-1&=0\\ 5-5y&=0 \end{cases} \end{align}\)
<=>\(\begin{align} \begin{cases} x&=1\\ y&=1 \end{cases} \end{align}\)
Suy ra: z=1+i =>|z|=\(\sqrt{2}\)
Đặt \(z=a+bi,\left(a,b\in R\right)\), khi đó :
\(2\left(z+1\right)=3\overline{z}+i\left(5-i\right)\Leftrightarrow2\left(a+bi+1\right)=3\left(a-bi\right)+1+5i\Leftrightarrow a-1+5\left(1-b\right)i=0\)
\(\Leftrightarrow\begin{cases}a=1\\b=1\end{cases}\) \(\Leftrightarrow\left|z\right|=\sqrt{2}\)