Tìm thể tích lớn nhất của hình chóp lục giác đều nội tiếp một mặt cầu bán kính bằng 1.
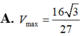
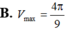
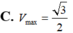
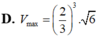
Trong các hình chóp lục giác đều nội tiếp trong mặt cầu bán kính bằng 1 thì hình chóp có thể tích Vmax bằng bao nhiêu?
A. Vmax = 16 3 27
B. Vmax = 3 2
C. Vmax = 3
D. Vmax = 4 3
Đáp án A

Gọi SH là đường cao hình chóp, a độ dài cạnh đáy và cũng là bán kính đường tròn ngoại tiếp đáy. Lúc đó tâm mặt cầu là I Î SH Þ SH = 1 + IH hoặc SH = 1 – IH.
Đặt IH = x (0 < x < 1) Þ a2 = 1 – x2, đáy hình chóp là ghép của 6 tam giác
![]()
 loại khi phải tìm Vmax).
loại khi phải tìm Vmax).
Có V’ = 0 Û x = 1 3
Trong tất cả các hình chóp tứ giác đều nội tiếp mặt cầu có bán kính bằng 9, tính thể tích của khối chóp có thể tích lớn nhất.
A. V=144
B.V=576 2
C.V=144 6
D.V=576
Trong tất cả các hình chóp tứ giác đều nội tiếp mặt cầu có bán kính bằng 9, tính thể tích V của khối chóp có thể tích lớn nhất.
A. V = 144
B. V = 576 2
C. V = 576
D. V = 144 6
Đáp án C
Gọi chiều cao của hình chóp là 9 + x , x ≥ 0 , cạnh của hình chóp là a , a ≤ 9 2
Diện tích đáy của hình chóp là: V = 1 3 .2 81 − x 2 9 + x = 2 3 9 − x = 2 3 9 − x 9 + x 9 + x
= 1 3 18 − 2 x 9 + x 9 + x = 1 3 ≤ 1 3 18 − 2 x + 9 + x + 9 + x 3 3 = 1 3 .12 3 = 576
Trong tất cả các hình chóp tứ giác đều nội tiếp mặt cầu có bán kính bằng 9, tính thể tích 𝑉 của khối chóp có thể tích lớn nhất.
A. V=144
B. V=576
C. V = 576 2
D. V = 144 6

Đáp án B
Ta có: R = S A 2 2 S O = 9
Suy ra S O 2 + O A 2 S O = 18
Mặt khác V S . A B C D = 1 3 S O . S A B C D = 1 3 S O . A C 2 2 = 2 3 S O . O A 2
= 2 3 S O . 18 S O − S O 2 . đặt S O = t 0 < t < 18 , xét hàm số
f t = 2 3 t 2 18 − t = 8 3 . t 2 . t 2 18 − t ≤ 8 3 t + 18 − t 3 3 = 576
Trong tất cả các hình chóp tứ giác đều nội tiếp mặt cầu có bán kính bằng 9, tính thể tích V của khối chóp có thể tích lớn nhất.
A. V = 144
B. V = 576 2
C. V = 576
D. V = 144 6
Trong các hình chóp tứ giác đều nội tiếp trong mặt cầu bán kính bằng 2 thì hình chóp có thể tích lớn nhất V m a x bằng bao nhiêu?
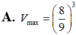
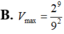
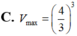
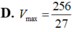
Trong tất cả các hình chóp tứ giác đều nội tiếp hình cầu có bán kính bằng 9. Tính thể tích V của khối chóp có thể tích lớn nhất.
![]()
![]()
![]()
![]()
Trong tất cả các hình chóp tứ giác đều nội tiếp hình cầu có bán kính bằng 9. Tính thể tích V của khối chóp có thể tích lớn nhất.
A. 144 2
B. 144.
C. 576 2
D. 576.
Tính thể tích lớn nhất của khối chóp tứ giác nội tiếp một mặt cầu bán kính bằng 3.
A. 49/3
B. 12 π
C. 32 π 3
D. 64/3
Đáp án D
Xét khối chóp tứ giác đều S.ABCD có chiều aco S H = h , A B = x
Bán kính mặt cầu ngoại tiếp khối chóp S.ABCD là R = S A 2 2 × S H = 3 ⇔ S A 2 = 6 × S H
Tam giác SAH vuông tại H, ta có S A 2 = S H 2 + A H 2 = S H 2 + A B 2 2 = h 2 + x 2 2
Suy ra h 2 + x 2 2 = 6 h ⇔ x 2 = 12 h − 2 h 2 .
Thể tích khối chóp S.ABCD là V = 1 3 . S H . S A B C D
Khi đó V = 1 3 h . x 2 = 2 3 h 6 h − h 2 = 2 3 6 h 2 − h 3 ≤ 64 3 (khảo sát hàm số)