Các câu hỏi tương tự
Tính thể tích lớn nhất của khối chóp tứ giác nội tiếp một mặt cầu bán kính bằng 3
A. 49 3
B. 12 π
C. 32 π 3
D. 64 3
Cho hình chóp tứ giác đều S.ABCD có khoảng cách từ A đến (SCD) bằng 4. Gọi V là thể tích khối chóp S.ABCD, tính giá trị lớn nhất của V. A.
32
3
B.
8
3
C.
16
3
D.
16
3
3
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có khoảng cách từ A đến (SCD) bằng 4. Gọi V là thể tích khối chóp S.ABCD, tính giá trị lớn nhất của V.
A. 32 3
B. 8 3
C. 16 3
D. 16 3 3
Trong tất cả các hình chóp tứ giác đều có d
3
là khoảng cách giữa hai đường thẳng chéo nhau gồm một đường thẳng chứa một đường chéo của đáy và đường thẳng còn lại chứa một cạnh bên hình chóp. Thể tích nhỏ nhất
V
m
i
n
của khối chóp là A.
V
...
Đọc tiếp
Trong tất cả các hình chóp tứ giác đều có d= 3 là khoảng cách giữa hai đường thẳng chéo nhau gồm một đường thẳng chứa một đường chéo của đáy và đường thẳng còn lại chứa một cạnh bên hình chóp. Thể tích nhỏ nhất V m i n của khối chóp là
A. V m i n =3
B. V m i n =9
C. V m i n = 9 3
D. V m i n =27
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 1, mặt bên SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích V của khối cầu ngoại tiếp hình chóp đã cho biết
A
S
B
^
120
0
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 1, mặt bên SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích V của khối cầu ngoại tiếp hình chóp đã cho biết A S B ^ = 120 0
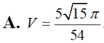
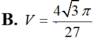
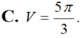
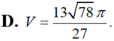
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 1, mặt bên SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích V của khối cầu ngoại tiếp hình chóp đã cho biết
A
S
B
^
120
0
A.
V
5
15...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 1, mặt bên SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích V của khối cầu ngoại tiếp hình chóp đã cho biết A S B ^ = 120 0
A. V = 5 15 π 54
B. V = 4 3 π 27
C. V = 5 π 3
D. V = 13 78 π 27
Cho hình chóp tứ giác đểu S.ABCD có cạnh đáy bằng a, thể tích khối chóp S.ABCD
V
a
3
3
18
. là V Góc giữa mặt bên và mặt phẳng đáy của hình chóp đã cho là? A.
60
0
B.
45...
Đọc tiếp
Cho hình chóp tứ giác đểu S.ABCD có cạnh đáy bằng a, thể tích khối chóp S.ABCD V = a 3 3 18 . là V Góc giữa mặt bên và mặt phẳng đáy của hình chóp đã cho là?
A. 60 0
B. 45 0
C. 30 0
D. 75 0
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a , SD tạo với mặt phẳng (SAC) một góc bằng
30
o
. Tính thể tích V của hình chóp S.ABCD.
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a , SD tạo với mặt phẳng (SAC) một góc bằng 30 o . Tính thể tích V của hình chóp S.ABCD.
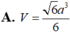
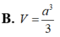
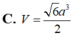

Cho khối chóp tứ giác đều có cạnh đáy bằng a và cạnh bên bằng
a
3
Tính thể tích V của khối chóp đó theo a:
Đọc tiếp
Cho khối chóp tứ giác đều có cạnh đáy bằng a và cạnh bên bằng a 3 Tính thể tích V của khối chóp đó theo a:
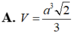
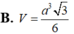
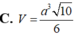
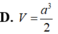
Xét hình chóp từ giác đều S.ABCD có tam giác SAC nội tiếp trong đường tròn có bán kính bằng 9. Gọi d là khoảng cách từ S đến mặt phẳng (ABCD) và T là diện tích tứ giác ABCD. Tính d khi biểu thức P = d. T đạt giá trị lớn nhất.
A. d =10
B. d =17
C. d =15
D. d =12