Tính thể tích V của khối trụ có bán kính đáy R, chiều cao là h.
A. V = πR 2 h
B. V = πRh 2
C. V = π 2 R h
D. V = 2 πRh
Những câu hỏi liên quan
Tính thể tích V của khối trụ có bán kính đáy r4 và chiều cao
h
4
2
A.
V
128
π
B.
V
64
2
π
C.
V
32
π
D.
V
32
2
π
Đọc tiếp
Tính thể tích V của khối trụ có bán kính đáy r=4 và chiều cao h = 4 2
A. V = 128 π
B. V = 64 2 π
C. V = 32 π
D. V = 32 2 π
Đáp án B
Áp dụng công thức tính thể tích khối trụ:
V = diện tích đáy x chiều cao
Đúng 0
Bình luận (0)
Thể tích V của khối trụ có bán kính đáy r 4 và chiều cao h
4
2
là:
Đọc tiếp
Thể tích V của khối trụ có bán kính đáy r = 4 và chiều cao h= 4 2 là:
Thể tích V của khối trụ có bán kính đáy r = 4 và chiều cao h = 4 2 là:
A. V = 32 π
B. V = 32 2 π
C. V = 64 2 π
D. V = 128 π
Chọn C.
Phương pháp:
Thể tích V của khối trụ có bán kính đáy r và chiều cao h là:
Đúng 0
Bình luận (0)
Cho hình trụ có bán kính đáy r2a và chiều cao
h
a
3
.
Tính thể tích V của khối trụ đã cho A.
V
π
a
3
3
B.
V
5
π
a
3
3
C. ...
Đọc tiếp
Cho hình trụ có bán kính đáy r=2a và chiều cao h = a 3 . Tính thể tích V của khối trụ đã cho
A. V = π a 3 3
B. V = 5 π a 3 3
C. V = 2 π a 3 3
D. V = 4 π a 3 3
Đáp án D
Thể tích khối trụ là V = π r 3 h = π . 2 a 2 . a 3 = 4 π a 3 3
Đúng 0
Bình luận (0)
Cho khối trụ có thể tích
V
16
π
và chiều cao gấp đôi bán kính đáy. Tính bán kính đáy r của khối trụ
Đọc tiếp
Cho khối trụ có thể tích V = 16 π và chiều cao gấp đôi bán kính đáy. Tính bán kính đáy r của khối trụ
Bán kính đáy của khối trụ tròn xoay có thể tích bằng V và chiều cao bằng h là A.
r
3
V
π
h
B.
r
3
V
2
π
h...
Đọc tiếp
Bán kính đáy của khối trụ tròn xoay có thể tích bằng V và chiều cao bằng h là
A. r = 3 V π h
B. r = 3 V 2 π h
C. r = V π h
D. r = 2 V π h
Một khúc gỗ có dạng khối nón có bán kính đáy r30cm, chiều cao h120cm. Anh thợ mộc chế tác khúc gỗ đó thành một khúc gỗ có dạng khối trụ như hình vẽ. Gọi V là thể tích lớn nhất của khúc gỗ dạng khối trụ có thể chế tác được. Tính V
Đọc tiếp
Một khúc gỗ có dạng khối nón có bán kính đáy r=30cm, chiều cao h=120cm. Anh thợ mộc chế tác khúc gỗ đó thành một khúc gỗ có dạng khối trụ như hình vẽ. Gọi V là thể tích lớn nhất của khúc gỗ dạng khối trụ có thể chế tác được. Tính V
Một khúc gỗ có dạng khối nón có bán kính đáy r 30 km, chiều cao h 120 km. Anh thợ mộc chế tác khúc gỗ đó thành một khúc gỗ có dạng khối trụ như hình vẽ. Gọi V là thể tích lớn nhất của khúc gỗ dạng khối trụ có thể chế tác được. Tính V A.
V
0
,
16
m
3
B.
V
0
,
024
m
3
C.
V...
Đọc tiếp
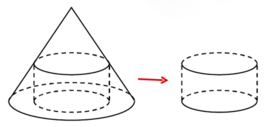
Một khúc gỗ có dạng khối nón có bán kính đáy r= 30 km, chiều cao h= 120 km. Anh thợ mộc chế tác khúc gỗ đó thành một khúc gỗ có dạng khối trụ như hình vẽ. Gọi V là thể tích lớn nhất của khúc gỗ dạng khối trụ có thể chế tác được. Tính V
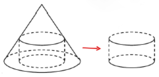
A. V = 0 , 16 m 3
B. V = 0 , 024 m 3
C. V = 0 , 027 m 3
D. V = 0 , 016 m 3
Đáp án D
Xét mặt cắt và lấy các điểm như hình vẽ bên cạnh.
Theo đề thì O A = O B = r = 30 cm và O H = h = 120 cm
Đặt O C = O D = R là bán kính đường tròn đáy của khúc gỗ khối trụ thì:
E C O H = A C O A = O A − O C O A ⇔ E C h = r − R R ⇔ E C = 4 30 − R
Thể tích khúc gỗ khối trụ là
V = π R 2 . E C = 4 π . R 2 . 30 − R ⇒ f R = 30 R 2 − R 3
Xét hàm số f R trên 0 ; 30 ⇒ max f R = 4000
Vậy thể tích lớn nhất của khối trụ V = 0 , 016 m 3
Đúng 0
Bình luận (0)
Một khúc gỗ có dạng khối nón có bán kính đáy r 30cm, chiều cao h 120cm. Anh thợ mộc chế tác khúc gỗ đó thành một khúc gỗ có dạng khối trụ như hình vẽ. Gọi V là thể tích lớn nhất của khúc gỗ dạng khối trụ có thể chế tác được. Tính V. A.
V
0
,
16
π
m
3
. B.
V
0
,
024
π...
Đọc tiếp
Một khúc gỗ có dạng khối nón có bán kính đáy r = 30cm, chiều cao h = 120cm. Anh thợ mộc chế tác khúc gỗ đó thành một khúc gỗ có dạng khối trụ như hình vẽ.
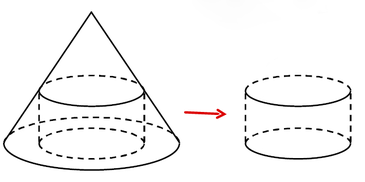
Gọi V là thể tích lớn nhất của khúc gỗ dạng khối trụ có thể chế tác được. Tính V.
A. V = 0 , 16 π m 3 .
B. V = 0 , 024 π m 3 .
C. V = 0 , 36 π m 3 .
D. V = 0 , 016 π m 3 .
Đáp án D
Gọi r 0 ; h 0 lần lượt là bán kính đáy và chiều cao của khối trụ.
Theo giả thuyết, ta có:
r 0 r = h − h 0 h ⇔ r 0 = 30. 120 − h 0 120 = 30 − h 0 4
Suy ra thể tích khối trụ là:
V = π r 0 2 . h 0 = π 30 − h 0 4 2 . h 0 = π . 120 − h 0 2 . h 0 16
Xét hàm số f t = t 120 − t 2 với t ∈ 0 ; 120 suy ra: max 0 ; 120 f t = 256000
Vậy thể tích lớn nhất của khối trụ là:
V max = π 256000 16 . 1 100 3 = 0 , 016 π c m 3
Đúng 0
Bình luận (0)