Có bao nhiêu số phức z = x + yi(x,y ∈ ℝ ) thỏa mãn x 2 + y 2 = 5 | x - 2 y | = 4 ?
A. Có 4 số
B. Có 2 số
C. Có 1 số
D. Không có số nào
Gọi M là điểm biểu diễn cho số phức z =x +yi(x,y ϵ ℝ) thỏa mãn |z +1 -2i|=|z|. Tập hợp điểm là đường thẳng nào sau đây?
A. 2x +4y +5 =0.
B. 2x -4y +5 =0.
C. 2x -4y +3 =0.
D. x -2y +1= 0
Cho z=x+yi với x , y ∈ ℝ là số phức thỏa mãn điều kiện z → + 2 - 3 i ≤ z + i - 2 ≤ 5 . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = x 2 + y 2 + 8 x + 6 y . Tính M+m.
A. 60 + 2 10
B. 156 6 - 20 10 .
C. 60 - 2 10 .
D. 156 5 + 20 10
Trên mặt phẳng phức, tập hợp các số phức z = x + y i x , y ∈ ℝ thỏa mãn z + 2 + i = z ¯ - 3 i là đường thẳng có phương trình
A. y = x + 1
B. y = - x + 1
C. y = - x - 1
D. y = x - 1
Xác định tập hợp các điểm trong mặt phẳng phức biểu diễn số phức z = x + i y , x , y ∈ ℝ thỏa mãn điều kiện z = 2 .
A. Đường tròn x 2 + y 2 = 4 .
B. Đường thẳng x = 2 .
C. Đường thẳng y = 2
D. Hợp hai đường thẳng x = 2, y = 2 .
Đáp án A
z = 2 ⇔ x 2 + y 2 = 2 ⇔ x 2 + y 2 = 4 .
Cho số phức z=x+yi, ( x , y ∈ R ) thỏa mãn z 3 = 18 + 26 i . Tính T = ( z - 2 ) 2017 + ( 4 - z ) 2017
A. T = 2 1009
B. T = 2 1010
C. T = 2 1011
D. T = 2 2012
Tìm số nguyên x, y sao cho số phức z = x + yi thỏa mãn z3 = 18 + 26i
A. 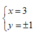
B. 
C. 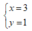
D. 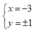
Chọn C.
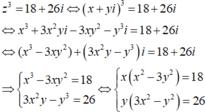
Do x; y nguyên nên
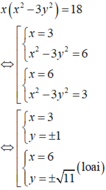
Mà y(3x2 – y2 ) = 26 ⇒ x = 3; y = 1.
Cho số phức z = x + y i x , y ∈ ℝ thỏa mãn z - 5 - 5 i = 2 2 . Tìm P = x + 2 y sao cho |z| nhỏ nhất
A. P = 12
B. P = 8
C. P = 9
D. P = 21
Trên mặt phẳng phức tập hợp các số phức z = x + yi thỏa mãn |z + 2 - i| = | z ¯ - 3i| là đường thẳng có phương trình
A. y = x + 1
B. y = -x + 1
C. y = -x - 1
D. y = x - 1
Gọi M là điểm biểu diễn số phức z = x + yi , x , y ∈ ℝ điểm biểu diễn số phức liên hợp của z bằng cách
A. Lấy đối xứng M qua trục tọa độ
B. Lấy đối xứng M qua trục hoành
C. Lấy đối xứng M qua đường thẳng y=x
D. Lấy đối xứng M qua trục tung
Đáp án B
Số phức liên hợp z ¯ = x − y i . Vậy điểm M′ biểu diễn z ¯ có được bằng cách lấy đối xứng z qua trục hoành.