Tìm tất cả các giá trị thực của tham số m để hệ 3 2 x + x + 1 - 3 2 + x + 1 + 2017 x ≤ 2017 x 2 - ( m + 2 ) x + 2 m + 3 ≥ 0 có nghiệm.
Những câu hỏi liên quan
Tìm tất cả các giá trị thực của tham số m để hệ
3
2
x
+
x
+
1
-
2
2...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hệ 3 2 x + x + 1 - 2 2 + x + 1 + 2017 x ≤ 2017 x 2 - ( m + 2 ) x + 2 m + 3 ≥ 0 có nghiệm
A. m ≤ - 2
B. m ≥ - 3
C. m > - 3
D. m ≥ - 2
Đáp án D.
Phương pháp:
Sử dụng phương pháp hàm số giải bất phương trình (1), suy ra điều kiện của nghiệm x.
Bất phương trình (2), cô lập m, đưa về dạng m ≥ f(x) trên [a;b] có nghiệm 
Cách giải: ĐK: x ≥ –1
Xét hàm số 
có 
=> Hàm số đồng biến trên R
Để hệ phương trình có nghiệm thì phương trình (2) có nghiệm 
Với 
Để phương trình có nghiệm 
(sử dụng MTCT để tìm GTNN)
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m để hệ
3
2
x
+
x
+
1
-
3
2
+...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hệ 3 2 x + x + 1 - 3 2 + x + 1 + 2017 x ⩽ 2017 x 2 - ( m + 2 ) x + 2 m + 3 ⩾ 0 có nghiệm.
A. m ≤ - 2
B. m ⩾ - 3
C. m > - 3
D. m ≥ - 2
Tìm tất cả các giá trị thực của tham số m để hệ bất phương trình
x
-
3
0
m
-
x
...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hệ bất phương trình x - 3 < 0 m - x < 1 vô nghiệm.
A. m < 4
B. m > 4
C. m ≤ 4
D. m ≥ 4
Chọn D
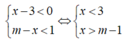
Hệ bất phương trình vô nghiệm khi và chỉ khi m - 1 ≥ 3 hay m ≥ 4
Đúng 0
Bình luận (0)
22 tháng 8 2021 lúc 20:21
Câu 1 : Tìm tất cả các giá trị của tham số thực m để hàm số \(y=mx^3-2mx^2+\left(m-2\right)x+1\) không có cực trị
Câu 2: Tìm tất cả các giá trị thực của tham số m để hàm số \(y=\left(m-1\right)x^4-2\left(m-3\right)x^2+1\) không có cực đại
Tìm tất cả các giá trị thực của tham số m để hệ bất phương trình
3
(
x
-
6
)
-
3
5
x
+...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hệ bất phương trình 3 ( x - 6 ) < - 3 5 x + m 2 > 7 có nghiệm.
A. m > -11.
B. m ≥ -11.
C. m < -11.
D. m ≤ -11.
Chọn A.
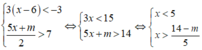
Hệ bất phương trình có nghiệm
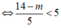⇔ 14 - m < 25 ⇔ -m < 11 ⇔ m > -11
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m để hệ bất phương trình
3
(
x
-
6
)
-
3
5
x
...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hệ bất phương trình
3 ( x - 6 ) < - 3 5 x + m 2 > 7 có nghiệm.
A. m > -11
B. m ≥ -11
C. m < -11
D. m ≤ -11
Chọn A
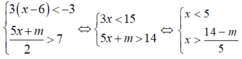
Hệ bất phương trình có nghiệm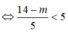 
hay 14 - m < 25 hay m > -11
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m để hệ bất phương trình
3
(
x
-
6
)
-
3
5
x
+...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hệ bất phương trình
3 ( x - 6 ) < - 3 5 x + m 2 > 7 có nghiệm.
A. m > -11
B. m ≥ -11
C. m < -11
D. m ≤ -11
Chọn A
Ta có:
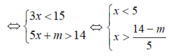
Hệ bất phương trình có nghiệm ⇔ 14 - m 5 < 5
Hay 14 - m < 25 tương đương m > -11
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m để hệ
3
2
x
+
x
+
1
-
3
2
+...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hệ 3 2 x + x + 1 - 3 2 + x + 1 + 2017 x ≤ 2017 x 2 - m + 2 x + 2 m + 3 ≥ 0 có nghiệm.
A. m ≥ - 3 .
B. m ≥ - 2 .
C. m > - 3 .
D. m ≤ - 2 .
Tìm tất cả các giá trị của tham số thực m để hệ phương trình
(
x
+
1
)
(
3
x
2
+
5
x
y
)...
Đọc tiếp
Tìm tất cả các giá trị của tham số thực m để hệ phương trình ( x + 1 ) ( 3 x 2 + 5 x y ) = m x 2 + 4 x + 5 y = 3 có ít nhất một cặp nghiệm thực
A . - 13 16 ; 9 4
B . ( - ∞ ; 9 4 ]
C . - ∞ ; 9 4
D . - 1 ; 9 4
