Tìm tất cả các số phức z thỏa mãn đồng thời hai điều kiện z = 2 và z 2 số thuần ảo.
A. z = 1 ± i h o ặ c z = - 1 ± i
B. z = 1 ± i
C. z = - 1 + i
D. z = - 1 - i
Có bao nhiêu số phức z thỏa mãn đồng thời hai điều kiện z = 2 và z 2 là số thuần ảo?
A. 2
B. Vô số
C. 0
D. 4
Tìm tất cả các số phức \(z\) thỏa mãn điều kiện:
\(\left|iz-1-3i\right|.\left|\overline{z}+1+i\right|=\left|z^2+\left(-6+2i\right)z+8-6i\right|\) và \(\dfrac{z-3}{z+2}\) là số thuần ảo.
Hỏi có bao nhiêu số phức z thỏa mãn đồng thời các điều kiện z - i = 5 và z 2 là số thuần ảo?
A. 2
B. 3
C. 0
D. 4
Hỏi có bao nhiêu số phức z thỏa mãn đồng thời điều kiện z − i = 4 và z là số thuần ảo?
A. 1.
B. 3.
C. 4.
D. 2.
Đáp án D
Gọi z = x + y i , x , y ∈ ℝ .
Ta có x 2 + y − 1 2 = 16, x = 0 ⇒ y = − 3 y = 5 .
Vậy có 2 số phức thỏa mãn đề bài
Có bao nhiêu số phức z thỏa mãn các điều kiện z - 2 + i = 2 v à ( z + i ) 2 là số thuần ảo?
Tìm số phức z thỏa mãn hai điều kiện:| z + 1 - 2i| = | z ¯ + 3 + 4i| và z - 2 i z ¯ + i là một số thuần ảo.
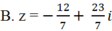
Chọn B.
Giả sử z = x + yi. Theo bài ra ta có: |x + 1 + (y – 2)i| = |x + 3 + (4 – y)i|
hay ( x + 1) 2+ ( y - 2) 2 = ( x + 3) 2 + ( y - 4) 2
suy ra y = x + 5
Số phức
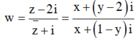
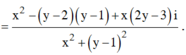
w là một số ảo
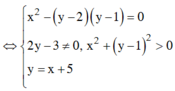
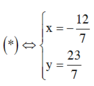
Vậy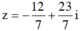 
Tìm tập hợp tất cả các giá trị của tham số m để có đúng 8 số phức z thỏa mãn đồng thời các điều kiện z + z ¯ + z - z ¯ = z 2 và z = m
Tìm tập hợp tất cả các giá trị của tham số m để có đúng 8 số phức z thỏa mãn đồng thời các điều kiện z + z ¯ + z - z ¯ = z 2 và z = m ?
D. 2 ; 2
B. 2 ; 2 2
C. 2 ; 2
D. 2 ; 2 2
Đặt z=x+yi ta có hệ đều kiện:
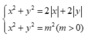
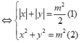
Ta có (1) là tập hợp các cạnh của hình vuông ABCD có tâm là gốc toạ độ độ dài cạnh bằng a = m 2 2 ; là đường tròn (C) có tâm là gốc toạ độ O bán kính bằng R = m.
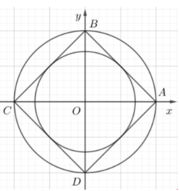
Để có đúng 8 số phức thoả mãn thì (C) phải nằm giữa đường tròn ngoại tiếp và đường tròn nội tiếp hình vuông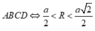 
Chọn đáp án D.
