Diện tích mặt cầu bán kính R bằng
![]()
![]()
![]()
![]()
Mặt cầu bán kính r có diện tích bằng 36 π . Tìm thể tích V của khối cầu bán kính r.
A. V = 72 2 π
B. V = 288 π
C. V = 36 π
D. V = 18 π
Diện tích mặt cầu bán kính R bằng
A. 4 πR 2
B. πR 2
C. 4 3 πR 2
D. 2 πR 2
Diện tích mặt cầu bán kính R bằng
A. 4 π R 2
B. 2 π R 2
C. π R 2
D. 4 3 π R 2
Diện tích mặt cầu bán kính R bằng
A. 4 3 π R 2 .
B. 4 π R 2 .
C. 2 π R 2 .
D. π R 2 .
Diện tích của mặt cầu có bán kính R bằng:
A. 2 πR 2
B. πR 2
C. 4 πR 2
D. 2 πR
Một hình trụ có hai đường tròn đáy nằm trên một mặt cầu bán kính R và có đường cao bằng bán kính mặt cầu. Diện tích toàn phần hình trụ đó bằng
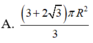
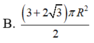
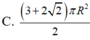
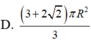
Chọn đáp án B
+ Gọi h, r lần lượt là chiều cao và bán kính đường tròn đáy của hình trụ.
Khi đó, bán kính mặt cầu ngoại tiếp hình trụ là
![]()
+ Theo bài ra, ta có h = r nên suy ra
![]()
+ Diện tích toàn phần hình trụ là:
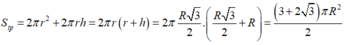
Một hình trụ có hai đường tròn đáy nằm trên một mặt cầu bán kính R và có đường cao bằng bán kính mặt cầu. Diện tích toàn phần hình trụ đó bằng
A. 3 + 2 3 πR 2 3
B. 3 + 2 3 πR 2 2
C. 3 + 2 2 πR 2 2
D. 3 + 2 2 πR 2 3
Chọn B.
Phương pháp: Coi đáy của hình trụ là mặt phẳng cắt mặt cầu. Áp dụng công thức

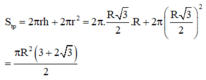
Một hình trụ có hai đường tròn đáy nằm trên một mặt cầu bán kính R và có đường cao bằng bán kính mặt cầu. Diện tích toàn phần hình trụ đó bằng:
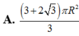
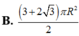
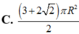
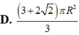
Một hình trụ có hai đường tròn đáy nằm trên một mặt cầu bán kính R và có đường cao bằng bán kính mặt cầu. Diện tích toàn phần hình trụ đó bằng
A. 3 + 2 3 πR 2 3
B. 3 + 2 3 πR 2 2
C. 3 + 2 2 πR 2 2
D. 3 + 2 2 πR 2 3
Đáp án B
Gọi h, r lần lượt là chiều cao và bán kính đường tròn đáy của hình trụ.
Khi đó, bán kính mặt cầu ngoại tiếp hình trụ là R 2 = r 2 + h 2 4
Theo bài ra, ta có h = R nên suy ra R 2 = r 2 + h 2 4 ⇔ r 2 = 3 R 2 4 ⇔ r = R 3 2
Diện tích toàn phần hình trụ là:
S t p = 2 πr 2 + 2 πrh = 2 πr r + h = 2 π . R 3 2 . R 3 2 + R = 3 + 2 3 πR 2 2 .