Các câu hỏi tương tự
Để tiết kiệm vật liệu nhất thì
S
t
p
nhỏ nhất
⇔
πR
2
π
R
⇒
R
1
⇒
h
2
Cho đồ thị hàm số yf(x) như hình vẽ dưới đây: Có bao nhiêu giá trị nguyên dương của tham số m để hàm số
y
f
(
x...
Đọc tiếp
Để tiết kiệm vật liệu nhất thì S t p nhỏ nhất ⇔ πR 2 = π R ⇒ R = 1 ⇒ h = 2 Cho đồ thị hàm số y=f(x) như hình vẽ dưới đây:
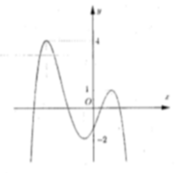
Có bao nhiêu giá trị nguyên dương của tham số m để hàm số y = f ( x - 2 ) - m 4 có 7 điểm cực trị.
A. 1
B. 2
C. 3
D. 4
Tính diện tích của mặt cầu có bán kính r=2
A. 32 π
B. 8 π
C. 2 π
D. 16 π
Tính diện tích S của mặt cầu có bán kính R = 2.
A. S = 32 π 3
B. S = 4 π
C. S = 8 π
D. S = 16 π
Trong hệ trục tọa độ cho 4 điểm A ( 1;1;-2 ), B ( 0;3;-2 ) ,C ( 0;0;1 ),I ( 0;1;0 ). D là một điểm bất kì thuộc mặt cầu tâm I, bán kính bằng 3. Khoảng cách từ D đến mặt phẳng (ABC) có giá trị lớn nhất bằng. A. 1 B.
6
C.
3
2
D. 2
Đọc tiếp
Trong hệ trục tọa độ cho 4 điểm A ( 1;1;-2 ), B ( 0;3;-2 ) ,C ( 0;0;1 ),I ( 0;1;0 ). D là một điểm bất kì thuộc mặt cầu tâm I, bán kính bằng 3. Khoảng cách từ D đến mặt phẳng (ABC) có giá trị lớn nhất bằng.
A. 1
B. 6
C. 3 2
D. 2
Trong không gian Oxyz, cho mặt cầu
S
:
(
x
−
4
)
2
+
(
y
+
5
)
2
+
(
z
−
3
)
2...
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu S : ( x − 4 ) 2 + ( y + 5 ) 2 + ( z − 3 ) 2 = 4 . Tìm tọa độ tâm I và bán kính R của mặt cầu.
A. I − 4 ; 5 ; − 3 v à R = 2
B. I 4 ; − 5 ; 3 v à R = 2
C. I − 4 ; 5 ; − 3 v à R = 4
D. I 4 ; − 5 ; 3 v à R = 4
Trong không gian với hệ tọa độ Oxyz, cho
A
1
;
2
;
-
3
,
B
3
2
;
3
2
;
-
1
2
,
C
1...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho A 1 ; 2 ; - 3 , B 3 2 ; 3 2 ; - 1 2 , C 1 ; 1 ; 4 , D 5 ; 3 ; 0 , Gọi S 1 là mặt cầu tâm A bán kính bằng 3, S 2 là mặt cầu tâm B bán kính bằng 3 2 . Có bao nhiêu mặt phẳng tiếp xúc với 2 mặt cầu S 1 , S 2 đồng thời song song với đường thẳng đi qua 2 điểm C D, .
A. 1
B. 2
C. 4
D. Vô số
Trong không gian với hệ tọa độ Oxyz, cho điểm
A
1
;
2
;
-
3
,
B
3
2
;
3
2
;
-
1
2
,
...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm A 1 ; 2 ; - 3 , B 3 2 ; 3 2 ; - 1 2 , C 1 ; 1 ; 4 , D 5 ; 3 ; 0 . Gọi S 1 là mặt cầu tâm A bán kính bằng 3, S 2 là mặt cầu tâm B bán kính bằng 3 2 Có bao nhiêu mặt phẳng tiếp xúc với 2 mặt cầu S 1 , S 2 đồng thời song song với đường thẳng đi qua 2 điểm C, D.
A. 1
B. 2
C. 3
D. Vô số
Mặt cầu bán kính r có diện tích bằng 36 π . Tìm thể tích V của khối cầu bán kính r.
A. V = 72 2 π
B. V = 288 π
C. V = 36 π
D. V = 18 π
Một hình cầu có bán kính bằng 2(m). Hỏi diện tích của mặt cầu bằng bao nhiêu A.
4
π
m
2
B.
16
π
m
2
C.
8
π
m
2
D.
π
m
2
Đọc tiếp
Một hình cầu có bán kính bằng 2(m). Hỏi diện tích của mặt cầu bằng bao nhiêu
A. 4 π m 2
B. 16 π m 2
C. 8 π m 2
D. π m 2
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu
S
tâm
I
1
;
-
2
;
1
; bán kính
R
4
và đường thẳng
d
:
x
2
y
-
1
-
2...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S tâm I 1 ; - 2 ; 1 ; bán kính R = 4 và đường thẳng d : x 2 = y - 1 - 2 = z + 1 - 1 . Mặt phẳng chứa d và cắt mặt cầu theo một đường tròn có diện tích nhỏ nhất. Hỏi trong các điểm sau điểm nào có khoảng cách đến mặt phẳng P lớn nhất.
A. O(0;0;0)
B. A 1 ; 3 5 ; - 1 4
C. (-1;-2;-3)
D. C(2;1;0)




