Trong không gian cho hai điểm A(x; y; z), B(m, n, p) thay đổi nhưng luôn thỏa mãn các điều kiện x 2 + y 2 + z 2 = 4, m 2 + n 2 + p 2 = 9. Vectơ AB → có độ dài nhỏ nhất là:
A. 5
B. 1
C. 13
D. Không tồn tại
Trong không gian cho hai điểm A, B cố định. Tập hợp tất cả các điểm M trong không gian thoả mãn ∠ A M B = 90 ° là
A. Mặt cầu đường kính AB
B. Mặt cầu đường kính AB nhưng bỏ đi hai điểm A, B
C. Khối cầu đường kính AB
D. Khối cầu đường kính AB nhưng bỏ đi hai điểm A, B
Trong không gian Oxyz, cho hai mặt phẳng α :2x+y-2z+1=0; β :x-2y+2z+3=0 Tập hợp tất cả các điểm trong không gian cách đều hai mặt phẳng đã cho là
A. Một mặt phẳng duy nhất
B. Một điểm duy nhất
C. Hai mặt phẳng phân biệt vuông góc với nhau
D. Một đường thẳng duy nhất song song với cả hai mặt phẳng đã cho
Điểm cần tìm M(x;y;z) ta có điều kiện cách đều hai mặt phẳng là
![]()
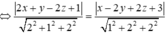
![]()
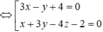
Vậy tập hợp các điểm này nằm trên hai mặt phẳng vuông góc với nhau (hai mặt phẳng này được gọi là mặt phẳng phân giác của góc tạo bởi hai mặt phẳng).
Chọn đáp án C.
Chọn đáp án C.
Trong không gian với hệ tọa độ Oxyz cho hai điểm A(3;3;1), B(0;2;1).và mặt phẳng (P): x + y + z - 7 = 0 . Đường thẳng d nằm trong (P) sao cho mọi điểm của d cách đều hai điểm A, B có phương trình là
A. x = t y = 7 + 3 t z = 2 t
B. x = 2 t y = 7 - 3 t z = t
C. x = t y = 7 - 3 t z = 2 t
D. x = - t y = 7 - 3 t z = 2 t
Phương trình mặt phẳng trung trực của AB là ![]()
Đường thẳng cần tìm d cách đều hai điểm A, B nên sẽ thuộc mặt phẳng α
Lại có ![]() hay
hay 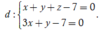
Chọn x = t ta được: 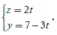
Chọn C.
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A 3 ; 3 ; 1 , B 0 ; 2 ; 1 và mặt phẳng P : x + y + z - 7 = 0 . Đường thẳng d nằm trong (P) sao cho mọi điểm của d cách đều hai điểm A, B có phương trình là
A. x = t y = 7 + 3 t z = 2 t
B. x = 2 t y = 7 - 3 t z = t
C. x = t y = 7 - 3 t z = 2 t
D. x = - t y = 7 - 3 t z = 2 t
Trong không gian Oxyz, cho hai điểm A 1 ; 2 ; − 3 ; B 2 ; 0 ; − 1 . Tìm giá trị của tham số m để hai điểm A, B nằm khác phía so với mặt phẳng x + 2 y + m z + 1 = 0
A. m ∈ 2 ; 3
B. m ∈ 2 ; 3
C. m ∈ − ∞ ; 2 ∪ 3 ; + ∞
D. m ∈ − ∞ ; 2 ∪ 3 ; + ∞
Đáp án B
Phương pháp:
-Sử dụng kiến thức về vị trí của một điểm đối với mặt phẳng.
Cho mặt phẳng P : A x + B y + C z + D = 0 và hai điểm

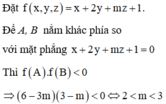
Trong không gian Oxyz, cho hai điểm A(1;2;-3), B(2 ;0 ;-1). Tìm giá trị của tham số m để hai điểm A, B nằm khác phía so với mặt phẳng x + 2 y + m z + 1 = 0 .
![]()
![]()
![]()
![]()
Đáp án B.
Phương pháp:
-Sử dụng kiến thức về vị trí của một điểm đối với mặt phẳng.
Cho mặt phẳng ![]()
và hai điểm ![]()
Đặt:
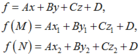
Hai điểm M, N nằm khác phía so với mặt phẳng (P)
![]()
Cách làm:
Đặt ![]()
Để A, B nằm khác phía so với mặt phẳng
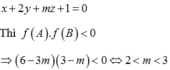
Trong không gian Oxyz, cho mặt phẳng ( P ) : x - y + 2 = 0 và hai điểm A ( 1 ; 2 ; 3 ) , B ( 1 ; 0 ; 1 ) . Điểm C a ; b ; - 2 sao cho tam giác ABC có diện tích nhỏ nhất. Tính a + b
A. 0
B. -3
C. 1
D. 2
Trong không gian Oxyz, cho hai điểm A(2;4;1), B(-1;1;3) và mặt phẳng (P): x-3y+2z-5=0. Viết phương trình mặt phẳng (Q) đi qua hai điểm A, B và vuông góc với mặt phẳng (P).
A. 2y+3z-10=0
B.2x+3z-11=0
C. 2y+3z-12=0
D. 2y+3z-11=0
Đáp án D
Ta có:
![]()
Khi đó:
![]()
Suy ra (Q): 2y+3z-11=0
Trong không gian Oxyz, cho hai điểm A(2;4;1); B(–1;1;3) và mặt phẳng (P): x -3y + 2z – 5 = 0. Viết phương trình mặt phẳng (Q) đi qua hai điểm A, B và vuông góc với mặt phẳng (P)
A. (Q): 2y + 3z – 10 = 0
B. (Q): 2x + 3z – 11 = 0
C. (Q): 2y + 3z – 12 = 0
D. (Q): 2y + 3z – 11 = 0
Đáp án D
Ta có: A B → = ( - 3 ; - 2 ; 2 ) ; n ( P ) → = ( 1 ; - 3 ; 2 )
Khi đó: A B → ; n ( P ) → = 0 ; 8 ; 12 ⇒ n ( Q ) → = ( 0 ; 2 ; 3 )
Suy ra (Q): 2y + 3z – 11 = 0
Trong không gian Oxyz, cho hai điểm A(1;3;-1), B(5;4;-4). Khoảng cách giữa hai điểm A và B là:
A. 16
B. 26
C. 2 2
D. 66