Nghịch đảo của số phức z = 4 + 3i là
A. 4-3i
B. 1 4 + 1 3 i
C. - 4 5 + 1 3 i
D. 4 25 - 3 25 i
Nghịch đảo của số phức z = 1 + i là
A. 1-i
B. -1+i
C. 1 2 + 1 2 i
D. 1 2 - 1 2 i
Nghịch đảo của số phức z = 1 + i là
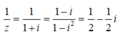
Chọn D
Phần thực và phần ảo của số phức z = (3 + 4i)(4 - 3i) + (2 - i)(3 + 2i) là
A. 32 và 8i
B. 32 và 8
C. 18 và -14
D. 32 và -8
Cho hai số phức z 1 = - 3 + 4 i , z 2 = 4 - 3 i . Môđun của số phức z = z 1 + z 2 + z 1 . z 2 là
A. 27
B. 27
C. 677
D. 677
Nghịch đảo của số phức z = 1 - 2i là
A. 2i - 1
B. -1 -2i
C. 1 5 - 2 5 i
D. 1 5 + 2 5 i
Môđun của số phức z=(-4+3i)i bằng:
A. 7
B.5
C.3
D.4
Môđun của tổng hai số phức z 1 = 3 - 4 i và z 2 = 4 + 3 i là
A. 5 2
B. 8
C. 10
D. 50
Trong số các số phức z thỏa mãn điều kiện z - 4 + 3 i = 3 gọi z 0 là số phức có mô đun lớn nhất. Khi đó z 0 là:
A. 3
B. 4
C. 5
D. 8
Đáp án D
Cách giải: gọi z=x+yi
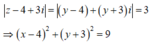
Vậy quỹ tích các điểm z thuộc đường tròn tâm I(4;-3); R=3
Đặt 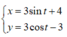
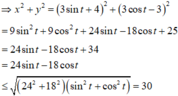
(theo bunhiacopxki)
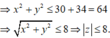
Trong số các số phức z thỏa mãn điều kiện |z-4+3i|=3, gọi z 0 là số phức có mô đun lớn nhất. Khi đó | z 0 | là:
A. 3
B. 4
C. 5
D. 8
Cho số phức z = -1 + 3i. Phần thực, phần ảo của z là
A. -1 và 3
B. -1 và -3
C. 1 và -3
D. -1 và -3i
Ta có z = -1 + 3i => z = - 1 - 3 i
Vậy phần thực và phần ảo của z− là -1 và -3.
Chọn đáp án B.