Cho biết có hai số phức z thỏa mãn z 2 = 119 - 120 i , kí hiệu là z 1 và z 2 .
Tính z 1 - z 2 2 .
A. 169
B. 114244
C. 338
D. 676
Cho biết có hai số phức z thỏa mãn z 2 = 119 - 120 i , ký hiệu z 1 và z 2 . Tính | z 1 - z 2 | 2 .
A. 169.
B. 114244.
C. 338.
D. 676.
Cho biết có hai số phức z thỏa mãn z 2 = 119 − 120 i , kí hiệu là z 1 và z 2 . Tính z 1 − z 2 2 .
A. 169
B. 114244
C. 388
D. 676
Cho biết có hai số phức z thỏa mãn z 2 = 119 - 120 i , kí hiệu là z 1 và z 2 . Tính z 1 - z 2 2
A. 169.
B. 114244.
C. 338.
D. 676.
Biết rằng hai số phức z 1 ; z 2 thỏa mãn z 1 - 3 - 4 i = 1 và z 2 - 3 - 4 i = 1 2 Số phức z có phần thực là a và phần ảo là b thỏa mãn 3a – 2b – 12 = 0. Giá trị nhỏ nhất của P = z - z 1 + z - 2 z 2 + 2 bằng
A. P m i n = 9945 11
B. P m i n = 5 - 2 3
C. P m i n = 9945 13
D. P m i n = 5 + 2 5
Biết rằng hai số phức z 1 , z 2 thỏa mãn z 1 − 3 − 4 i = 1 và z 2 − 3 − 4 i = 1 2 . Số phức z có phần thực là a và phần ảo là b thỏa mãn 3 a − 2 b − 12 = 0 . Giá trị nhỏ nhất của P = z − z 1 + z − 2 z 2 + 2 bằng:
A. P min = 9945 11 .
B. P min = 5 − 2 3 .
C. P min = 9945 13 .
D. P min = 5 + 2 5 .
Biết rằng hai số phức z 1 , z 2 thỏa mãn | z 1 - 3 - 4 i | = 1 và | z 2 - 3 - 4 i | = 1 2 . Số phức z có phần thực là a và phần ảo là b thỏa mãn 3 a - 2 b = 12 . Giá trị nhỏ nhất của P = | z - z 1 | + | z - 2 z 2 | + 2 bằng:
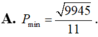
![]()
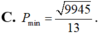
![]()
Cho các số phức z thỏa mãn |z – 2 – 4i| = 2. Gọi z1; z2 số phức có module lớn nhất và nhỏ nhất. Tổng phần ảo của hai số phức bằng?
A. 8i
B. 4
C. -8
D. 8
Chọn D.
Ta có ![]()
![]()
+ Giá trị lớn nhất của |z| là ![]() đạt được tại
đạt được tại

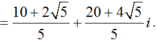
+ Giá trị nhỏ nhất của |z| là ![]() , đạt được tại
, đạt được tại
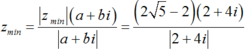
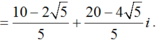
Vậy tổng phần ảo là: 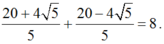
Biết rằng hai số phức z 1 , z 2 thỏa mãn z 1 - 3 - 4 i = 1 và z 2 - 3 - 4 i = 1 2 . Số phức z có phần thực là a và phần ảo là b thỏa mãn 3 a - 2 b = 12 . Giá trị nhỏ nhất của biểu thức P = z - z 1 + z - z 2 + 2 bằng
A. P m i n = 3 1105 11
B. P m i n = 5 - 2 3
C. P m i n = 3 1105 13
D. P m i n = 5 + 2 5
Chọn đáp án C
Gọi M 1 , M 2 , M lần lượt là điểm biểu diễn của các số phức z 1 , 2 z 2 , z trên mặt phẳng tọa độ Oxy.
Do z 1 - 3 - 4 i = 1 nên quỹ tích điểm M 1 là đường tròn C 1 có tâm I 1 3 ; 4 và bán kính R = 1
Do z 2 - 3 - 4 i = 1 2 ⇔ 2 z 2 - 6 - 8 i = 1 nên quỹ tích điểm M 2 là đường tròn C 2 có tâm I 2 6 ; 8 và bán kính R = 2
Ta có điểm M(a; b) thỏa mãn 3a - 2b = 12 nên quỹ tích điểm M là đường thẳng d: 3x - 2y - 12 = 0
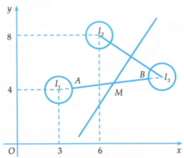
Khi đó
![]()
Gọi C 3 là đường tròn đối xứng với đường tròn C 2 qua đường thẳng d.
Ta tìm được tâm của C 3 là I 3 138 13 ; 64 13 và bán kính R = 1
Khi đó
![]()
với M 3 ∈ C 3 và A, B lần lượt là giao điểm của đường thẳng I 1 I 3 với hai đường tròn C 1 , C 3 (quan sát hình vẽ).
Dấu "=" xảy ra khi và chỉ khi M 1 ≡ A và M 3 ≡ B
Vậy P m i n = A B + 2 = I 1 I 3 = 3 1105 13
Cho số phức z thỏa mãn ( 1 - 3i) z là số thực và ![]() . Hỏi có bao nhiêu số phức z thỏa mãn
. Hỏi có bao nhiêu số phức z thỏa mãn
A. 1
B. 2
C. 3
D. 4
Chọn B.
Gọi số phức cần tìm là z = a + bi.
Ta có ( 1 - 3i) z = ( 1 - 3i) ( a + bi)
= a + 3b - 3ai + bi = a + 3b + ( b - 3a) i
+ Do ( 1 - 3i) z là số thực nên b - 3a = 0 hay b = 3a
+ ta có ![]() ⇔|a – 2 + (-b + 5)i| = 1
⇔|a – 2 + (-b + 5)i| = 1
Hay ( a - 2) 2 + ( 5 - 3a) 2 = 1
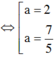 (thỏa mãn)
(thỏa mãn)
Vậy có hai số phức z thỏa mãn là z = 2 + 6i và z = 7/5 + 21/5i