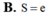
Tính diện tích hình phẳng giới hạn bởi y=(x+1)*e^x , trục hoành và các đường thẳng x=-2,x=0
\(\left(x+1\right)e^x=0\Rightarrow x=-1\)
\(S=\int\limits^0_{-2}\left|\left(x+1\right)e^x\right|dx=-\int\limits^{-1}_{-2}\left(x+1\right)e^xdx+\int\limits^0_{-1}\left(x+1\right)e^xdx\)
\(=\dfrac{2e-2}{e^2}\)
Tính diện tích hình phẳng giới hạn bởi các đường y = x e x , trục hoành, đường thẳng x = 0 và x = 1
A. S = e + 1
B. S = e
C. S = 1
D. S = e - 1
Đáp án C
Diện tích hình phẳng cần tính là
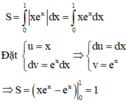
Tính diện tích hình phẳng giới hạn bởi các đường y=xe x , trục hoành, đường thẳng x=0 và x=1
A. S = e − 1
B. S = e
C. S = 1
D. S = e + 1
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y = e x - e - x , trục hoành, đường thẳng x = -1 và đường thẳng x = 1.
A. e + 1 e - 2
B. 0
C. 2 e + 1 e - 2
D. e + 1 e
Biết diện tích hình phẳng giới hạn bởi đường cong y=f(x),y=0,x=0,x=2a bằng S. Diện tích hình phẳng giới hạn bởi đường cong y=f(2x), trục hoành Ox và hai đường thẳng x=0,x=a bằng
A. S/4.
B. 4S.
C. 2S.
D. S/2.
Biết diện tích hình phẳng giới hạn bởi đường cong y=f(x), y=0, x=2a bằng S. Diện tích hình phẳng giới hạn bởi đường cong y=f(2x), trục hoành Ox và hai đường thẳng x=0, x=a bằng:
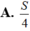
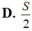
Tính diện tích hình phẳng giới hạn bởi : Đồ thị hàm số y = e x +1 , trục hoành , đường thẳng x = 0 và đường thẳng x = 1
A.e
B. 2+e
C.e-1
D.2e+1
Tính diện tích hình phẳng giới hạn bởi các đường:
y = ln x ; x = 1 e ; x = e và trục hoành.
Diện tích hình phẳng giới hạn bởi đường cong y=f(x), trục hoành và hai đường thẳng x=0; x=1 là
A. π ∫ 0 1 f 2 x d x
B. ∫ 0 1 f 2 x d x
B. ∫ 0 1 f x d x
D. ∫ 0 1 f x d x
