Hàm số nào sau đây nghịch biến trên khoảng xác định của nó?
A. y = x 5
B. y = log 0 , 5 x
C. y = log 3 x
D. y = 5 x
Cho hàm số: y = x - 2 x + 3
Khẳng định nào sau đây là đúng?
A. Hàm số đồng biến trên từng khoảng xác định;
B. Hàm số đồng biến trên khoảng (- ∞ ;+ ∞ );
C. Hàm số nghịch biến trên từng khoảng xác định;
D. Hàm số nghịch biến trên khoảng (- ∞ ;+ ∞ ).
Cho hàm số y=f(x) xác định trên ℝ và có đồ thị của hàm số f’(x) và các khẳng định sau:
(1). Hàm số y=f(x) đồng biến trên khoảng 1 ; + ∞
(2). Hàm số y=f(x) nghịch biến trên khoảng - ∞ ; - 2
(3). Hàm số y=f(x) nghịch biến trên khoảng - 2 ; 1 .
(4). Hàm số y = f x 2 đồng biến trên khoảng - 1 ; 0
(5). Hàm số y = f x 2 nghịch biến trên khoảng (1;2)

Số khẳng định đúng là
A. 4
B. 3
C. 2
D. 5
Hàm số nào sau đây nghịch biến trên từng khoảng xác định của nó?
A. y = x - 1 x + 1
B. y = 2 x + 1 x - 3
C. y = x - 2 2 x - 1
D. y = x - 3 x - 2
Chọn đáp án B
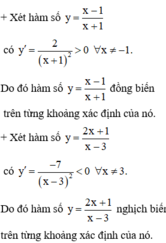
Ta chọn đáp án B. (Độc giả tự kiểm tra hai hàm số còn lại).
Hàm số nào sau đây nghịch biến trên mỗi khoảng xác định của nó?
A. y = - x + 2 x + 2
B. y = x - 2 - x + 2
C. y = x - 2 x + 2
D. y = x + 2 - x + 2
Hàm số nào sau đây nghịch biến trên mỗi khoảng xác định của nó?
A. y = x - 2 - x + 2
B. y = x - 2 x + 2
C. y = - x + 2 x + 2
D. y = x + 2 - x + 2
Hàm số nào sau đây nghịch biến trên mỗi khoảng xác định của nó?
A. y = - x + 2 x + 2
B. y = x - 2 - x + 2
C. y = x - 2 x + 2
D. y = x + 2 - x + 2
Chọn: A
Xét đáp án A ta có:
![]()
và y ' = - 4 x + 2 2 < 0 ∀ x ∈ D
Vậy hàm số y = - x + 2 x + 2 nghịch biến trên mỗi khoảng xác định của nó.
Hàm số nào sau đây nghịch biến trên mỗi khoảng xác định của nó?
A. y = x - 2 - x + 2
B. y = x - 2 x + 2
C. y = - x + 2 x + 2
D. y = x + 2 - x + 2
Cho hàm số:
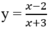
Khẳng định nào sau đây là đúng?
A. Hàm số đồng biến trên từng khoảng xác định;
B. Hàm số đồng biến trên khoảng (- ∞ ;+ ∞ );
C. Hàm số nghịch biến trên từng khoảng xác định;
D. Hàm số nghịch biến trên khoảng (- ∞ ;+ ∞ ).
Với giá trị nào của m thì hàm số y = x + m x - 1 nghịch biến trên từng khoảng xác định của nó
A. m < - 1
B. m ≤ - 1
C. m > - 1
D. m ≥ - 1