Hình hộp chữ nhật có ba kích thước a,2a,3a có thể tích bằng
A. 2a3
B. 6 a3
C. 12 a3
D. 3 a3
Những câu hỏi liên quan
Cho hình hộp ABCD.ABCD có đáy là hình chữ nhật, hình chiếu của A lên đáy (ABCD) trùng với trung điểm của cạnh AD. Biết rằng AB a, AD 2a và thể tích hình hộp đã cho bằng 2
a
3
. Khoảng cách từ B đến mặt phẳng (ADCB) bằng:A.
2
a
6
B.
2...
Đọc tiếp
Cho hình hộp ABCD.A'B'C'D' có đáy là hình chữ nhật, hình chiếu của A' lên đáy (ABCD) trùng với trung điểm của cạnh AD. Biết rằng AB = a, AD = 2a và thể tích hình hộp đã cho bằng 2 a 3 . Khoảng cách từ B đến mặt phẳng (A'DCB') bằng:
A. 2 a 6 B. 2 a 3
C. 3 a 3 D. a 2
Chọn D.
Gọi H là trung điểm của cạnh AD. Kẻ HI vuông góc với A'D tại I. Khi đó d(B,(A'DCB')) = d(A,(A'DCB')) = 2d(H,(A'DCB')) = 2HI.
Đúng 0
Bình luận (0)
Hình hộp chữ nhật có ba kích thước
a
;
2
a
;
3
a
có thể tích bằng: A.
2
a
3
B.
6
a
3
C.
12
a
3
D.
3
a
3
Đọc tiếp
Hình hộp chữ nhật có ba kích thước a ; 2 a ; 3 a có thể tích bằng:
A. 2 a 3
B. 6 a 3
C. 12 a 3
D. 3 a 3
Cho hình hộp chữ nhật
A
B
C
D
.
A
B
C
D
có
A
B
a
,
A
D
a
3
và
C
C
2
a
. Khối trụ ngoại tiếp hình hộp chữ nhật đã cho có thể tích bằng A.
8
πa
3
B....
Đọc tiếp
Cho hình hộp chữ nhật A B C D . A ' B ' C ' D ' có A B = a , A D = a 3 và C C ' = 2 a . Khối trụ ngoại tiếp hình hộp chữ nhật đã cho có thể tích bằng
A. 8 πa 3
B. 2 3 πa 3
C. 2 πa 3
D. 4 πa 3
Chọn đáp án C.
Bán kính đáy của khối trụ ngoại tiếp hình hộp chữ nhật đã cho là
Đúng 0
Bình luận (0)
Một hình nón có đường kính đáy là 2a
π
3, góc ở đỉnh 120
°
. Thể tích của khối nón đó theo a là:A. 2
3
π
a
3
B. 3
π
a
3
C.
π
a
3
D.
π...
Đọc tiếp
Một hình nón có đường kính đáy là 2a π 3, góc ở đỉnh 120 ° . Thể tích của khối nón đó theo a là:
A. 2 3 π a 3 B. 3 π a 3
C. π a 3 D. π a 3 3
Chọn C.
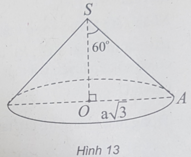
(h.13) Gọi S là đỉnh hình nón, O là tâm đáy, A là một điểm thuộc đường tròn đáy.
Theo giả thiết, đường tròn đáy có bán kính R = OA = a 3 và ∠ = 60 °
Trong tam giác SOA vuông tại O, ta có: OA = SO.tan60 ° ⇒ SO = a.
Do đó chiều cao của hình nón là h = a.
Vậy thể tích hình nón là: V = π a 3
Đúng 0
Bình luận (0)
Cho hình lập phương ABCD.A'B'C'D' cạnh bằng a. Khi đó thể tích hình chóp A.A'BCD' bằng:
A. a 3 /2 B. a 3 /3
C. a 3 /4 D. a 3 /6
Chọn B.
Hình nón A.A'BCD' với đáy là hình chữ nhật A'BCD' có diện tích S = A'B.BC = a 2 √2 và chiều cao h = (a 2 )/2 nên có thể tích V = a 3 /3
Đúng 0
Bình luận (0)
Thể tích của khối hộp chữ nhật có các kích thước lần lượt là a, 2a, 3a bằng. A.
6
a
3
B.
6
a
2
C.
2
a
3
D.
3
a
3
2
5
Đọc tiếp
Thể tích của khối hộp chữ nhật có các kích thước lần lượt là a, 2a, 3a bằng.
A. 6 a 3
B. 6 a 2
C. 2 a 3
D. 3 a 3 2 5
Thể tích của khối hộp chữ nhật có các kích thước lần lượt là a, 2a, 3a bằng. A.
6
a
3
B.
6
a
2
C.
2
a
3
D.
3
a
2
2
5
Đọc tiếp
Thể tích của khối hộp chữ nhật có các kích thước lần lượt là a, 2a, 3a bằng.
A. 6 a 3
B. 6 a 2
C. 2 a 3
D. 3 a 2 2 5
Đáp án A
Thể tích hình hộp chữ nhật bằng tích ba kích thước
V = a . 2 a . 3 a = 6 a 3
Đúng 0
Bình luận (0)
Câu 6: Khối là một nhóm ô liền kề nhau tạo thành hình chữ nhật. Theo em trong trang tính khối có thể là:
A. A3:B5 B. A3:A5 C. A3:B3 D. Cả A, B và C
Xem thêm câu trả lời
Cho hình hộp đứng ABCD.A¢B¢C¢D¢ có AB a, AD
2
a
, BD
a
3
. Góc tạo bởi AB¢ và mặt phẳng (ABCD) bằng
60
o
.
Tính thể tích của khối chóp D¢.ABCD. A.
3
3
a
3
.
B.
3
a
2
.
C....
Đọc tiếp
Cho hình hộp đứng ABCD.A¢B¢C¢D¢ có AB = a, AD = 2 a , BD = a 3 . Góc tạo bởi AB¢ và mặt phẳng (ABCD) bằng 60 o . Tính thể tích của khối chóp D¢.ABCD.
A. 3 3 a 3 .
B. 3 a 2 .
C. a 3 .
D. 2 3 3 a 3 .
