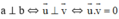Vector nào dưới đây là 1 vector chỉ phương của đường thẳng song song với trục Ox:
A. u ⇀ = 1 ; 0
B. u ⇀ = 1 ; - 1
C. u ⇀ = 1 ; 1
D. u ⇀ = 0 ; 1
Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng song song với trục Ox?
![]()
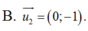
![]()
![]()
Đáp án A
Trục Ox có phương trình tổng quát là: y= 0.
Đường thẳng này có VTPT là ( 0; 1) và VTCP là (1; 0)
Các đường thẳng song song với trục Ox sẽ có cùng VTPT và có cùng VTCP với trục Ox. Nên đường thẳng song song với trục Ox có VTCP là (1; 0) .
Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng song song với trục Ox?
A.(1; 0)
B. (0; 1)
C.(1; 1)
D.Tất cả sai
Đáp án A
Trục Ox có phương trình là y= 0.
Nên đường thẳng này có 1 VTPT là: n → ( 0 ; 1 )
Do đó 1 VTCP của đường thẳng là (1; 0)
Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng song song với trục Oy?
A. (1; 0)
B.(0; -1)
C. (1; 1)
D. (-1; 1)
Đáp án B
Trục Oy có phương trình là x = 0.
Nên đường thẳng này có 1 VTPT là n → ( 1 ; 0 )
Do đó:1 VTCP của đường thẳng là (0; 1)
Mà 2 vectơ (0; 1) và (0; -1) là 2 vectơ cùng phương nên vectơ (0; -1) cũng là VTCP đối với trục Oy.
Vectơ nào dưới đây là một vectơ pháp tuyến của đường thẳng song song với trục Ox?
A. (0; 1)
B. (1; 0)
C. (-1; 1)
D. (1; 1)
Đáp án A
Trục Ox có phương trình đường thẳng là y = 0. Đường thẳng này có VTPT là (0; 1).
Các đường thắng song song với nhau sẽ có cùng VTCP và có cùng VTPT nên các đường thẳng song song với trục Ox có VTPT là (0; 1) .
Trong không gian Oxyz, cho đường thẳng d : x + 2 4 = y − 1 − 4 = z + 2 3 và mặt phẳng P : 2 x − y + 2 z + 1 = 0. Đường thẳng ∆ đi qua E − 2 ; 1 ; − 2 , song song với (P) đồng thời tạo với d góc bé nhất. Biết rằng ∆ có một vector chỉ phương u → m ; n ; 1 . Tính T = m 2 − n 2
A. T = − 5
B. T = 4
C. T = 3
D. T = − 4
Trong không gian Oxyz, cho đường thẳng d : x + 2 4 = y - 1 - 4 = z + 2 3 và mặt phẳng (P): 2x-y+2z+1=0. Đường thẳng ∆ đi qua E(-2;1;-2) song song với (P) đồng thời tạo với d góc bé nhất. Biết rằng ∆ có một vector chỉ phương u → = ( m ; n ; 1 ) . Tính T = m 2 - n 2
A. T = -5
B. T = 4
C. T = 3
D. T = -4
Đáp án D
Phương pháp:
![]()
+) Sử dụng công thức
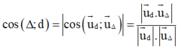
+) Để góc giữa ∆ và d là nhỏ nhất thì
![]()
Cách giải :
![]()
Do ∆ //(P)
![]()
Ta có
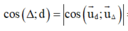
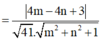
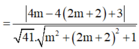
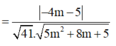
Để góc giữa ∆ và d là nhỏ nhất thì
![]()
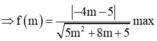
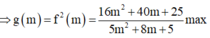
Có g'(x)
= ( 32 m + 40 ) ( 5 m 2 + 8 m + 5 ) - ( 16 m 2 + 40 m + 25 ) ( 10 m + 8 ) 5 m 2 + 8 m + 5 2
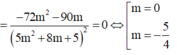
Lập BBT ta thấy
![]()
![]()
Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A(1;-2;-3), B(-1;4;1) và đường thẳng d : x + 2 1 = y - 2 1 = z + 3 2 . Phương trình nào dưới đây là phương trình đường thẳng đi qua trung điểm của đoạn AB và song song với d?
A. ∆ : x 1 = y - 1 1 = z + 1 2
B. ∆ : x 1 = y - 2 - 1 = z + 2 2
C. ∆ : x 1 = y - 1 - 1 = z + 1 2
D. ∆ : x - 1 1 = y - 1 - 1 = z + 1 2
Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A(1;-2;-3), B(-1;4;1) và đường thẳng d : x + 2 1 = y - 2 1 = z + 3 2 . Phương trình nào dưới đây là phương trình đường thẳng đi qua trung điểm của đoạn AB và song song với d?
![]()
![]()
![]()
![]()
Trong không gian hai đường thẳng không cắt nhau có thể vuông góc với nhau không? Giả sử hai đường thẳng a và b lần lượt có vectơ chỉ phương là vector u → và vector v → . Khi nào ta có kết luận a và b vuông góc với nhau?
+ Trong không gian, hai đường thẳng chéo nhau vẫn có thể vuông góc với nhau.
Đường thẳng a có vectơ chỉ phương u →
Đường thẳng b có vectơ chỉ phương v →